实验北校举行运动会，组委会招墓了16名男志愿者和14名女志愿者，调查发现，男、女志愿者中分别有10 人和6人喜爱运动，其余不喜爱.
（1）根据以上数据完成以下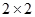
列联表：
（2）根据列联表的独立性检验，有多大的把握认为性别与喜爱运动有关？
(3)从不喜爱运动的女志愿者中和喜爱运动的女志愿者中各选1人，求其中不喜爱运动的女生甲及喜爱运动的女生乙至少有一人被选取的概率．
参考公式 ：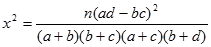
（其中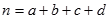
）
| |
 |
 |
 |
 |
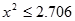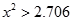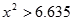| 是否有关联 |
没有关联 |
90% |
95% |
99% |
（本小题10分）已知在三棱锥S--ABC中，∠ACB=900，又SA⊥平面ABC，
AD⊥SC于D，求证：AD⊥平面SBC，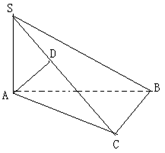
某电器公司生产A型电脑。1993年这种电脑每台平均生产成本为5 000元，并以纯利润20%确定出厂价。从1994年开始，公司通过更新设备和加强管理，使生产成本逐年降低。到1997年，尽管A型电脑出厂价仅是1993年的80%，但却实现了50%纯利润的高效益。
（1）求1997年每台A型电脑的生产成本；
（2）以1993年的生产成本为基数，求1993～1997年生产成本平均每年降低的百分数（精确到0.01，以下数据可供参考：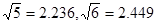
）。
如图，已知底角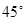
的等腰梯形ABCD，底边BC长为7cm,腰长为
cm，当一条垂直于底边BC（垂足为F）的直线l从左至右移动（与梯形ABCD有公共点）时，直线l把梯形分成两部分，令BF=
，试写出左边部分的面积
与的函数解析式，并画出大致图象。
已知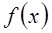
是定义在R上的奇函数，且当
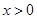时，f(x)=log2x求
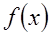的解析式。
已知函数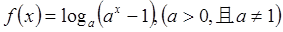
，
（1）求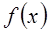
的定义域；（2）讨论函数
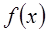的单调性。