（本小题满分12分）已知函数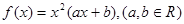
在
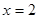时有极值，其图象在点
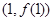处的切线与直线
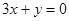平行．
（1）求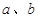
的值和函数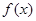
的单调区间；
（2）若当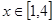
时，恒有
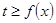，试确定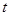
的取值范围．
连续抛掷两枚骰子，观察落地后骰子向上的点数．
（1）求这个试验的基本事件总数；
（2）写出“点数之和等于
”这个事件包含的所有基本事件；
（3）求“点数之和等于
”这一事件的概率．
某市统计的2006～2009年新生儿出生数及其中男婴数（单位：人）见下表：
| 时间 |
2006年 |
2007年 |
2008年 |
2009年 |
| 出生婴儿数 |
21840 |
23072 |
20094 |
19982 |
| 出生男婴数 |
11453 |
12031 |
10297 |
10242 |
（1）试计算男婴的出生频率（精确到0.001）；
（2）该市男婴出生的概率约是多少？
一场篮球比赛到了最后5分钟，甲队比乙队少得5分。如果甲队全投3分球，则有8次投篮机会。如果甲队全投2分球，则有3次投篮机会。假设甲队队员投3分球的命中率均为0.6，投2分球的命中率均为0 .8，并且甲队加强防守，不给乙队投篮机会．问全投3分球与全投2分球这两种方案中选择哪一种甲队获胜的概率较大？
在三种产品，合格率分别是0.90,0.95和0.95，各抽取一件进行检验.
（１）求恰有一件不合格的概率；
（２）求至少有两件不合格的概率.（精确到0.001）
有12齿和8齿的齿轮衔接在一起旋转，其中各有一齿磨损，现准备进行检修，求拆下来时，
（1）恰巧两个磨损的衔接在一起的概率；
（2）衔接的两齿中至少有一个磨损的概率．