如图,在四棱锥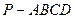 中,底面ABCD是正方形,侧棱
中,底面ABCD是正方形,侧棱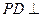 底面ABCD,
底面ABCD,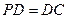 ,E是PC的中点.
,E是PC的中点.
(1)证明 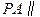 平面
平面 ;
;
(2)求EB与底面ABCD所成的角的正切值.
|
 (
( )
)
(1)求 的定义域;
的定义域;
(2)问是否存在实数 、
、 ,当
,当 时,
时, 的值域为
的值域为 ,且
,且 若存在,求出
若存在,求出 、
、 的值,若不存在,说明理由.
的值,若不存在,说明理由.
已知函数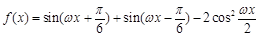 (
( ,
, )
)
(1)求 的值域;
的值域;
(2)若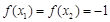 ,且
,且 的最小值为
的最小值为 ,求
,求 的递增区间.
的递增区间.
已知偶函数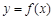 满足:当
满足:当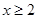 时,
时, ,
,
当 时,
时,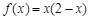
(1) 求当 时,
时,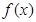 的表达式;
的表达式;
(2) 试讨论:当实数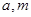 满足什么条件时,函数
满足什么条件时,函数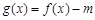 有4个零点,
有4个零点,
且这4个零点从小到大依次构成等差数列.
已知函数
(I)如果对任意 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
(II)设函数 的两个极值点分别为
的两个极值点分别为 判断下列三个代数式:
判断下列三个代数式:
① ②
② ③
③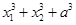 中有几个为定值?并且是定值请求出;
中有几个为定值?并且是定值请求出;
若不是定值,请把不是定值的表示为函数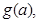 并求出
并求出 的最小值.
的最小值.
对于函数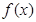 ,若存在
,若存在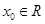 ,使
,使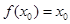 ,则称
,则称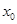 是
是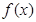 的一
的一
个"不动点".已知二次函数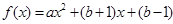
(1)当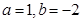 时,求函数
时,求函数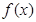 的不动点;
的不动点;
(2)对任意实数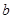 ,函数
,函数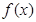 恒有两个相异的不动点,求
恒有两个相异的不动点,求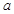 的取值范围;
的取值范围;
(3)在(2)的条件下,若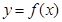 的图象上
的图象上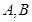 两点的横坐标是
两点的横坐标是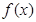 的不动点,
的不动点,
且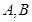 两点关于直线
两点关于直线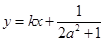 对称,求
对称,求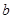 的最小值.
的最小值.