(本小题满分12分)
某品牌的汽车4S店,对最近100位采用分期付款的购车者进行统计,统计结果如下表所示:已知分3期付款的频率为0.2,4S店经销一辆该品牌的汽车 ,顾客分1期付款,其利润为1万元,分2期或3期付款其利润为1.5万元;分4期或5期付款,其利润为2万元,用
,顾客分1期付款,其利润为1万元,分2期或3期付款其利润为1.5万元;分4期或5期付款,其利润为2万元,用 表示经销一辆汽车的利润。
表示经销一辆汽车的利润。
| 付款方工 |
分1期 |
分2期 |
分3期 |
分4期 |
分5期 |
| 频数 |
40 |
20 |
 |
10 |
 |
(1)求上表中的 值;
值;
(2)若以频率作为概率,求事件A:“购买该品牌汽车的3位顾客中,至多有1位采用3期付款”的频率P(A);
(3)求 的分布列及数学期望E
的分布列及数学期望E 。
。
甲,乙,丙三位学生独立地解同一道题,甲做对的概率为 ,乙,丙做对的概率分别为
,乙,丙做对的概率分别为 ,
,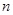 (
( >
>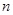 ),且三位学生是否做对相互独立.记
),且三位学生是否做对相互独立.记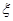 为这三位学生中做对该题的人数,其分布列为:
为这三位学生中做对该题的人数,其分布列为:
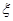 |
0 |
1 |
2 |
3 |
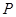 |
 |
 |
 |
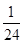 |
(Ⅰ)求至少有一位学生做对该题的概率;
(Ⅱ)求 ,
,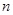 的值;
的值;
(Ⅲ)求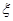 的数学期望.
的数学期望.
已知向量 =(
=(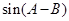 ,
, ),
), =(1,
=(1, ),且
),且

 =
=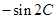 ,其中
,其中 、
、 、
、 分别为
分别为 的三边
的三边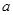 、
、 、
、 所对的角.
所对的角.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)若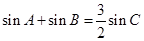 ,且
,且 ,求边
,求边 的长.
的长.
已知 ,函数
,函数
(1)求曲线 在点
在点 处的切线方程; (2)当
处的切线方程; (2)当 时,求
时,求 的最大值.
的最大值.
知椭圆 的左右焦点为F1,F2,离心率为
的左右焦点为F1,F2,离心率为 ,以线段F1 F2为直径的圆的面积为
,以线段F1 F2为直径的圆的面积为 , (1)求椭圆的方程;(2) 设直线l过椭圆的右焦点F2(l不垂直坐标轴),且与椭圆交于A、B两点,线段AB的垂直平分线交x轴于点M(m,0),试求m的取值范围.
, (1)求椭圆的方程;(2) 设直线l过椭圆的右焦点F2(l不垂直坐标轴),且与椭圆交于A、B两点,线段AB的垂直平分线交x轴于点M(m,0),试求m的取值范围.
已知 ,点
,点 在曲线
在曲线 上
上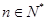 ,
, (Ⅰ)(Ⅰ)求数列
(Ⅰ)(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设数列 的前n项和为
的前n项和为 ,若对于任意的
,若对于任意的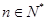 ,使得
,使得 恒成立,求最小正整数t的值.
恒成立,求最小正整数t的值.