已知数列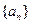 的前
的前
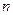 项和为
项和为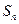 ,且
,且
(1)求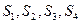 的值;
的值;
(2)猜想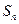 的表达式,并用数学归纳法加以证明。
的表达式,并用数学归纳法加以证明。
在 中,
中, ,
, ,
, 分别为内角
分别为内角 ,
, ,
, 的对边,且
的对边,且 .
.
(1)求 ;
;
(2)若 ,
, ,求
,求 .
.
已知椭圆 :
: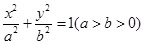 的离心率为
的离心率为 ,其长轴长与短轴长的和等于6.
,其长轴长与短轴长的和等于6.
(1)求椭圆 的方程;
的方程;
(2)如图,设椭圆 的上、下顶点分别为
的上、下顶点分别为 ,
,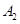 ,
, 是椭圆上异于
是椭圆上异于 ,
,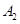 的任意一点,直线
的任意一点,直线 ,
,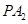 分别交
分别交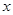 轴于点
轴于点 ,
,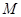 ,若直线
,若直线 与过点
与过点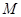 ,
, 的圆
的圆 相切,切点为
相切,切点为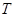 ,证明:线段
,证明:线段 的长为定值.
的长为定值.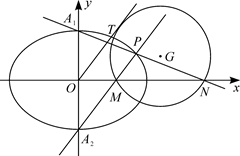
数列 满足
满足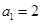 ,
,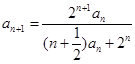 (
(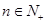 ).
).
(1)设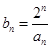 ,求数列
,求数列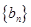 的通项公式
的通项公式 ;
;
(2)设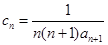 ,数列
,数列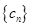 的前
的前 项和为
项和为 ,求出
,求出 并由此证明:
并由此证明: <
< .
.
如图,在四棱锥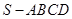 中,侧棱
中,侧棱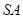 ⊥底面
⊥底面 ,
, ,
, ,
,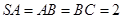 ,
,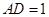 ,
, 是棱
是棱 的中点.
的中点.
(1)求证: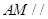 面
面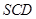 ;
;
(2)设点 是线段
是线段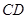 上的一点,且
上的一点,且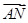 在
在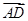 方向上的射影为
方向上的射影为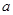 ,记
,记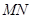 与面
与面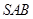 所成的角为
所成的角为 ,问:
,问: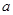 为何值时,
为何值时,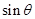 取最大值?
取最大值?
在三角形 中,
中, ,
, ,
, 的对边分别为
的对边分别为 ,
, ,
, ,且
,且
(1)求 ;
;
(2)若 ,求
,求 的取值范围.
的取值范围.