(本小题满分13分)
已知函数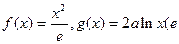 为自然对数的底数)
为自然对数的底数)
(1)求 的单调区间,若
的单调区间,若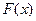 有最值,请求出最值;
有最值,请求出最值;
(2)是否存在正常数 ,使
,使 的图象有且只有一个公共点,且在该公共点处有共同的切线?若存在,求出
的图象有且只有一个公共点,且在该公共点处有共同的切线?若存在,求出 的值,以及公共点坐标和公切线方程;若不存在,请说明理由。
的值,以及公共点坐标和公切线方程;若不存在,请说明理由。
设命题 :函数
:函数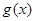 =
= 是
是 上的减函数,命题
上的减函数,命题 :函数
:函数 的定义域为
的定义域为 ,若“
,若“ 且
且 ”为假命题,“
”为假命题,“ 或
或 ”为真命题,求实数
”为真命题,求实数 的取值范围.
的取值范围.
(本小题满分14分)
已知函数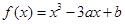 在
在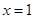 处有极小值
处有极小值 。
。
(1)求函数 的解析式;
的解析式;
(2)若函数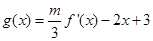 在
在 只有一个零点,求
只有一个零点,求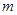 的取值范围。
的取值范围。
(本小题满分14分)
已知,圆C: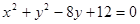 ,直线
,直线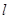 :
: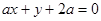 .
.
(1) 当a为何值时,直线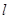 与圆C相切;
与圆C相切;
(2) 当直线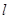 与圆C相交于A、B两点,且
与圆C相交于A、B两点,且 时,求直线
时,求直线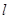 的方程.
的方程.
(本小题满分14分)
已知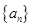 是首项为19,公差为-4的等差数列,
是首项为19,公差为-4的等差数列,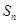 为
为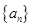 的前
的前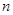 项和.
项和.
(Ⅰ)求通项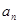 及
及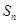 ;
;
(Ⅱ)设 是首项为1,公比为2的等比数列,求数列
是首项为1,公比为2的等比数列,求数列 的通项公式及其前
的通项公式及其前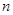 项和
项和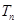 .
.
如图,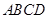 是正方形,
是正方形, 是正方形的中心,
是正方形的中心,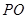
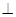 底面
底面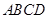 ,
,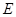 是
是 的中点.
的中点.
求证:(1)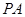 //平面
//平面 ;(2)平面
;(2)平面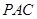
 平面
平面 .
.