(本小题满分13分)
已知三棱锥P-ABC中,PA⊥ABC,AB⊥AC,PA=AC= AB,N为AB上一点,AB=4AN,M,S分别为PB,BC的中点.
AB,N为AB上一点,AB=4AN,M,S分别为PB,BC的中点.
(Ⅰ)证明:CM⊥SN;
(Ⅱ)求SN与平面CMN所成角的大小.
(本小题满分14分)
给定椭圆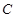 :
: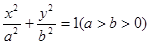 . 称圆心在原点
. 称圆心在原点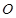 ,半径为
,半径为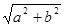 的圆是椭圆
的圆是椭圆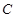 的“准圆”. 若椭圆
的“准圆”. 若椭圆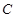 的一个焦点为
的一个焦点为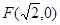 ,其短轴上的一个端点到
,其短轴上的一个端点到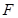 的距离为
的距离为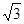 .
.
(1)求椭圆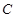 的方程和其“准圆”方程;
的方程和其“准圆”方程;
(2)点 是椭圆
是椭圆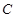 的“准圆”上的一个动点,过动点
的“准圆”上的一个动点,过动点 作直线
作直线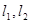 ,使得
,使得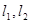 与椭圆
与椭圆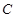 都只有一个交点,试判断
都只有一个交点,试判断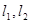 是否垂直?并说明理由.
是否垂直?并说明理由.
(本小题满分12分)
定义在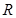 上的函数
上的函数 同时满足以下条件:
同时满足以下条件:
① 在
在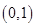 上是减函数,在
上是减函数,在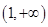 上是增函数;②
上是增函数;②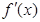 是偶函数;
是偶函数;
③ 在
在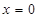 处的切线与直线
处的切线与直线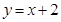 垂直.
垂直.
(1)求函数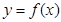 的解析式;
的解析式;
(2)设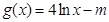 ,若存在
,若存在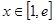 ,使
,使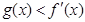 ,求实数
,求实数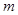 的取值范围.
的取值范围.
(本小题满分12分)
如图所示,四棱锥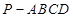 中,
中, 为正方形,
为正方形, ,
,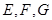 分别是线段
分别是线段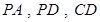 的中点. 求证:
的中点. 求证:
(1) //平面
//平面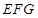 ;
;
(2)平面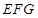 ⊥平面
⊥平面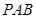 .
.
(本小题满分12分)
某产品按行业生产标准分成 个等级,等级系数
个等级,等级系数 依次为
依次为 ,其中
,其中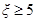 为标准
为标准 ,
, 为标准
为标准 ,产品的等级系数越大表明产品的质量越好. 已知某厂执行标准
,产品的等级系数越大表明产品的质量越好. 已知某厂执行标准 生产该产品,且该厂的产品都符合相应的执行标准.从该厂生产的产品中随机抽取
生产该产品,且该厂的产品都符合相应的执行标准.从该厂生产的产品中随机抽取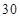 件,相应的等级系数组成一个样本,数据如下:
件,相应的等级系数组成一个样本,数据如下:
3 5 3 3 8 5 5 6 3 4
6 3 4 7 5 3 4 8 5 3
8 3 4 3 4 4 7 5 6 7
该行业规定产品的等级系数 的为一等品,等级系数
的为一等品,等级系数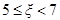 的为二等品,等级系数
的为二等品,等级系数 的为三等品.
的为三等品.
(1)试分别估计该厂生产的产品的一等品率、二等品率和三等品率;
(2)从样本的一等品中随机抽取2件,求所抽得2件产品等级系数都是8的概率.
(本小题满分12分)
已知数列 满足
满足 ,
,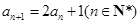 .
.
⑴求证:数列 是等比数列,并写出数列
是等比数列,并写出数列 的通项公式;
的通项公式;
⑵若数列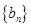 满足
满足 ,求
,求 的值.
的值.