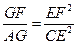已知椭圆
的中心为直角坐标系
的原点,焦点在
轴上,它的一个顶点到两个焦点的距离分别是7和1.
(Ⅰ)求椭圆
的方程;
(Ⅱ)若
为椭圆
上的动点,
为过
且垂直于
轴的直线上的点,
,求点
的轨迹方程,并说明轨迹是什么曲线。
(本小题满分13分)
如图,已知正三棱柱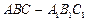 的底面正三角形的边长是2,D是
的底面正三角形的边长是2,D是 的中点,直线
的中点,直线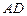 与侧面
与侧面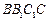 所成的角是
所成的角是 .
.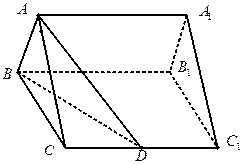
⑴求二面角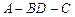 的大小;
的大小;
⑵求点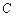 到平面
到平面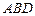 的距离.
的距离.
(本小题满分13分)
甲、乙、丙三人按下面的规则进行乒乓球比赛:第一局由甲、乙参加而丙轮空,以后每一局由前一局的获胜者与轮空者进行比赛,而前一局的失败者轮空.比赛按这种规则一直进行到其中一人连胜两局或打满6局时停止.设在每局中参赛者胜负的概率均为 ,且各局胜负相互独立.求:
,且各局胜负相互独立.求:
(Ⅰ)打满3局比赛还未停止的概率;
(Ⅱ)比赛停止时已打局数 的分布列与期望E
的分布列与期望E .
.
.
(本小题满分13分)
已知函数
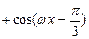
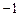 (
( ),且函数
),且函数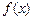 的最小正周期为
的最小正周期为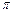 .
.
⑴求函数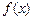 的解析式;
的解析式;
⑵在△ 中,角
中,角 所对的边分别为
所对的边分别为 .若
.若 ,
, ,且
,且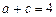 ,试求
,试求 的值.
的值.
(23)(本小题满分10分)选修4-4:坐标系与参数方程
已知直线C1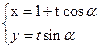 (t为参数),C2
(t为参数),C2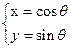 (
( 为参数),
为参数),
(Ⅰ)当 =
=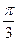 时,求C1与C2的交点坐标;
时,求C1与C2的交点坐标;
(Ⅱ)过坐标原点O作 C1的垂线,垂足为A,P为OA中点,当 变化时,求P点的轨迹的参数方程,并指出它是什么曲线.
变化时,求P点的轨迹的参数方程,并指出它是什么曲线.
请考生在第(22)、(23)、(24)三题中任选一题作答,如果多做,则按所做的第一题记分。做答时用2B铅笔在答题卡上把所选题目的题号涂黑。
(22)(本小题满分10分)选修4-1:几何证明选讲
如图,已经⊙O和⊙M相交于A、B两点,AD为⊙M的直径,直线BD交⊙O于点C,点G为弧BD中点,连结AG分别交⊙O、BD于点E、F,连结CE.
(Ⅰ) 求证:AG·EF=CE·GD;
(Ⅱ) 求证: