(本小题满分13分)
甲、乙、丙三人按下面的规则进行乒乓球比赛:第一局由甲、乙参加而丙轮空,以后每一局由前一局的获胜者与轮空者进行比赛,而前一局的失败者轮空.比赛按这种规则一直进行到其中一人连胜两局或打满6局时停止.设在每局中参赛者胜负的概率均为 ,且各局胜负相互独立.求:
,且各局胜负相互独立.求:
(Ⅰ)打满3局比赛还未停止的概率;
(Ⅱ)比赛停止时已打局数 的分布列与期望E
的分布列与期望E .
.
(本小题满分12分)
已知投资某项目的利润与产品价格的调整有关,在每次调整中价格下降的概率都是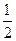 .设该项目产品价格在一年内进行2次独立的调整,记产品价格在一年内的下降次数为
.设该项目产品价格在一年内进行2次独立的调整,记产品价格在一年内的下降次数为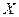 ,对该项目每投资十万元,
,对该项目每投资十万元,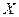 取0、1、2时,一年后相应的利润为1.6万元、2万元、2.4万元.求投资该项目十万元,一年后获得利润的数学期望及方差.
取0、1、2时,一年后相应的利润为1.6万元、2万元、2.4万元.求投资该项目十万元,一年后获得利润的数学期望及方差.
(本小题满分10分)
某班组织知识竞赛,已知题目共有10道,随机抽取3道让某人回答,规定至少要答对其中2道才能通过初试,他只能答对其中6道,试求:
(1)抽到他能答对题目数的分布列;
(2)他能通过初试的概率。
已知抛物线 :
: 上一点
上一点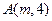 到其焦点的距离为
到其焦点的距离为 .
.
(I)求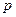 与
与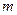 的值;
的值;
(II)设抛物线 上一点
上一点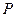 的横坐标为
的横坐标为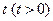 ,过
,过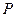 的直线交
的直线交 于另一点
于另一点 ,交
,交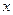 轴于点
轴于点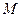 ,过点
,过点 作
作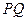 的垂线交
的垂线交 于另一点
于另一点 .若
.若 是
是 的切线,求
的切线,求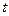 的最小值.
的最小值.
如图所示,在直四棱柱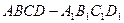 中,
中,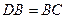 ,
,  ,点
,点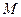 是棱
是棱 上一点.
上一点.
(Ⅰ)求证: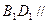 面
面 ;
;
(Ⅱ)求证: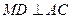 ;
;
(Ⅲ)试确定点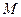 的位置,使得平面
的位置,使得平面
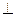 平面
平面 .
.
设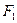 、
、 分别是椭圆
分别是椭圆 的左、右焦点.
的左、右焦点.
(Ⅰ)若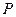 是该椭圆上的一个动点,求
是该椭圆上的一个动点,求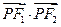 的最大值和最小值;
的最大值和最小值;
(Ⅱ)设过定点 的直线
的直线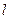 与椭圆交于不同的两点
与椭圆交于不同的两点 、
、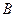 ,且∠
,且∠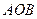 为钝角(其中
为钝角(其中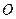 为坐标原点),求直线
为坐标原点),求直线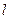 的斜率
的斜率 的取值范围.
的取值范围.