已知AB、CD是两平行平面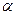 、
、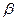 内的异面线段,AB=
内的异面线段,AB=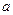 ,CD=
,CD=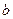 ,它们所成的角为
,它们所成的角为 .平面
.平面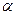 、
、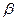 的距离为
的距离为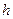 .求证:不论AB、CD在
.求证:不论AB、CD在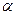 、
、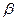 内如何移动,三棱锥
内如何移动,三棱锥 的体积不变,并用
的体积不变,并用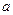 ,
,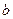 ,
,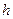 ,
, 表示体积.
表示体积.
如图,已知点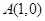 ,
,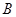 是单位圆
是单位圆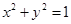 上一动点,且点
上一动点,且点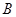 是线段
是线段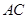 的中点.
的中点.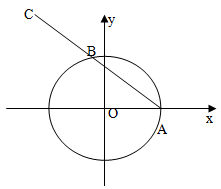
(1)若点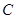 在
在 轴的正半轴上,求
轴的正半轴上,求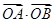 ;
;
(2)若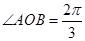 ,求点
,求点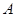 到直线
到直线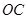 的距离.
的距离.
已知函数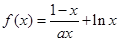 在
在 上是增函数,且
上是增函数,且 .
.
(1)求 的取值范围;
的取值范围;
(2)求函数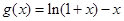 在
在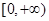 上的最大值;
上的最大值;
(3)设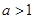 ,
,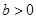 ,求证:
,求证: .
.
已知函数 满足
满足 且在
且在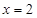 时函数取得极值.
时函数取得极值.
(1)求 的值;
的值;
(2)求函数 的单调区间;
的单调区间;
(3)求函数 在区间
在区间 上的最大值
上的最大值 的表达式.
的表达式.
已知数列 满足
满足 ,
,
(1)求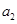 ,
, ,
, ,
,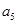 ;
;
(2)归纳猜想出通项公式 ,并且用数学归纳法证明;
,并且用数学归纳法证明;
(3)求证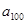 能被15整除.
能被15整除.
某校举办安全法规知识竞赛,从参赛的高一、高二学生中各抽出100人的成绩作为样本.对高一年级的100名学生的成绩进行统计,得到成绩分布的频率分布直方图如图:
(1)若规定60分以上(包括60分)为合格,计算高一年级这次知识竞赛的合格率;
(2)将上述调查所得到的频率视为概率.现在从该校大量高一学生中,采用随机抽样方法每次抽取1名学生,抽取3次,记被抽取的3名学生中的合格人数为 .若每次抽取的结果是相互独立的,求
.若每次抽取的结果是相互独立的,求 的分布列和期望
的分布列和期望 ;
;
| 高一 |
高二 |
合计 |
|
| 合格人数 |
|||
| 不合格人数 |
|||
| 合计 |
(3)若高二年级这次知识竞赛的合格率为60%,由以上统计数据填写2×2列联表,并问是否有99%的把握认为“这次知识竞赛的成绩与年级有关系” .