已知函数 满足
满足 且在
且在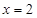 时函数取得极值.
时函数取得极值.
(1)求 的值;
的值;
(2)求函数 的单调区间;
的单调区间;
(3)求函数 在区间
在区间 上的最大值
上的最大值 的表达式.
的表达式.
(本小题满分12分)已知椭圆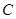 :
: 的离心率为
的离心率为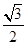 ,右顶点
,右顶点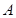 是抛物线
是抛物线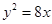 的焦点.
的焦点.
(Ⅰ)求椭圆的方程;
(Ⅱ)是否存在过点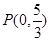 的直线
的直线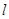 与椭圆交于
与椭圆交于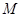 ,
,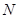 两个不同的点,且使
两个不同的点,且使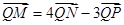 成立(
成立( 为直线
为直线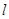 外的一点)?若存在,求出
外的一点)?若存在,求出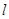 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
如图,三棱柱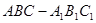 中,
中, ⊥面
⊥面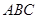 ,
, ,
, ,
, 为
为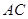 的中点.
的中点.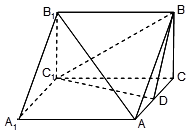
(Ⅰ)求证: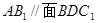 ;
;
(Ⅱ)求二面角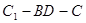 的余弦值;
的余弦值;
(Ⅲ)在侧棱 上是否存在点
上是否存在点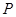 ,使得
,使得 ?请证明你的结论.
?请证明你的结论.
(本小题满分12分)清华大学自主招生考试题中要求考生从A,B,C三道题中任选一题作答,考试结束后,统计数据显示共有600名学生参加测试,选择A,B,C三题答卷数如下表:
| 题 |
A |
B |
C |
| 答卷数 |
180 |
300 |
120 |
(Ⅰ)负责招生的教授为了解参加测试的学生答卷情况,现用分层抽样的方法从600份答案中抽出若干份答卷,其中从选择A题作答的答卷中抽出了3份,则应分别从选择B,C题作答的答卷中各抽出多少份?
(Ⅱ)测试后的统计数据显示,A题的答卷得优的有60份,若以频率作为概率,在(Ⅰ)问中被抽出的选择A题作答的答卷中,记其中得优的份数为 ,求
,求 的分布列及其数学期望
的分布列及其数学期望 .
.
在梯形 中,
中,

(Ⅰ)求 的长;
的长;
(Ⅱ)若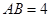 ,求梯形
,求梯形 的面积.
的面积.
(本小题满分14分)若 是公差不为
是公差不为 的等差数列
的等差数列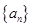 的前
的前 项和,且
项和,且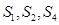 成等比数列。
成等比数列。
(1)求等比数列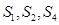 的公比;
的公比;
(2)若 ,求
,求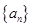 的通项公式;
的通项公式;
(3)设 ,
,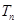 是数列
是数列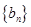 的前
的前 项和,求使得
项和,求使得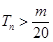 对所有
对所有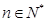 都成立的最大正整数
都成立的最大正整数