设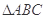 的内角
的内角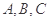 所对的边分别为
所对的边分别为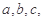 且
且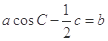 .
.
(1)求角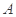 的大小;
的大小;
(2)若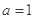 ,求
,求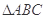 的周长的取值范围.
的周长的取值范围.
已知函数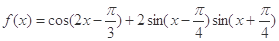
(1)求函数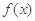 的最小正周期和图象的对称轴方程;
的最小正周期和图象的对称轴方程;
(2)求函数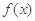 在区间
在区间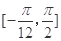 上的值域.
上的值域.
已知函数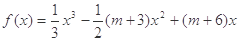 ,x∈R.(其中m为常数).
,x∈R.(其中m为常数).
(1)当 时,求函数的极值点和极值;
时,求函数的极值点和极值;
(2)若函数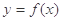 在区间(0,+∞)上有两个极值点,求实数
在区间(0,+∞)上有两个极值点,求实数 的取值范围.
的取值范围.
如图,在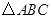 中,
中, ,点
,点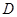 在
在 边上,且
边上,且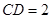 ,
, .
.
(1)求 ;
;
(2)求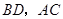 的长.
的长.
设等差数列 的前
的前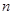 项和为
项和为 ,且
,且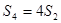 ,
,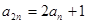 。
。
(1)求数列 的通项公式;
的通项公式;
(2)设数列 的前
的前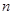 项和为
项和为 ,且
,且 (其中
(其中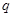 是非零的实数),若
是非零的实数),若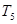 ,
, ,
,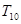 成等差数列,问
成等差数列,问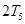 ,
,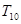 ,
,  能成等比数列吗?说明理由;
能成等比数列吗?说明理由;
(3)设数列 的通项公式
的通项公式 ,是否存在正整数
,是否存在正整数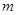 、
、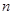 (
(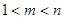 ),使得
),使得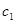 ,
, ,
,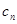 成等比数列?若存在,求出所有
成等比数列?若存在,求出所有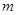 、
、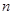 的值;若不存在,说明理由。
的值;若不存在,说明理由。