已知椭圆 的离心率
的离心率 ,短轴长为
,短轴长为 .
.
(Ⅰ)求椭圆方程;(Ⅱ)若椭圆与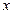 轴正半轴、
轴正半轴、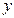 轴正半轴的交点分别为
轴正半轴的交点分别为 、
、 ,经过点
,经过点 且斜率为
且斜率为 的直线
的直线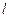 与椭圆交于不同的两点
与椭圆交于不同的两点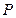 、
、 .是否存在常数
.是否存在常数 ,使得向量
,使得向量 共线?如果存在,求
共线?如果存在,求 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
已知函数 的一部分图像如右图所示,(其中
的一部分图像如右图所示,(其中 ,
, ,
, ).
).
(Ⅰ)求函数 的解析式并求函数的单调递增区间;
的解析式并求函数的单调递增区间;
(Ⅱ)在 中,角
中,角 ,
, ,
, 所对的边长分别为
所对的边长分别为 ,
, ,
, ,若
,若 ,
, ,
, 的面
的面
积为 ,求边长
,求边长 的值.
的值.
已知各项均不相等的等差数列 的前四项和
的前四项和 ,且
,且 ,
, ,
, 成等比数列.
成等比数列.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设 为数列
为数列 的前
的前 项和,若
项和,若 对一切
对一切 恒成立,求实数
恒成立,求实数 的最小值.
的最小值.
某市为调研高三一轮复习质量,在2014年10月份组织了一次摸底考试,并从某校2015届高三理科学生在该次考试的数学成绩进行分析,利用分层抽样抽取90分以上的1200名学生的成绩进行分析,已知该样本的容量为20,分数用茎叶图记录如图所示(部分数据丢失),得到的频率分布表如下:
| 分数段 |
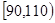 |
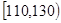 |
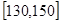 |
| 频数 |
4 |
||
| 频率 |
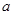 |
0.45 |
0.2 |

(Ⅰ)求表中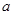 的值及分数在
的值及分数在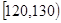 范围内的学生人数;
范围内的学生人数;
(Ⅱ)从得分在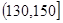 内的学生随机选2名学生的得分,求2名学生的平均分不低于140分的概率.
内的学生随机选2名学生的得分,求2名学生的平均分不低于140分的概率.
(本小题满分7分) 选修4—5:不等式选讲
已知关于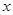 的不等式:
的不等式: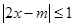 的整数解有且仅有一个值为2.
的整数解有且仅有一个值为2.
(Ⅰ)求整数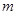 的值;
的值;
(Ⅱ)已知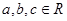 ,若
,若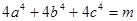 ,求
,求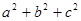 的最大值
的最大值
(本小题满分7分)选修4-4:坐标系与参数方程
在直角坐标系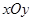 中,直线
中,直线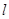 的方程为
的方程为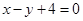 ,曲线
,曲线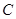 的参数方程
的参数方程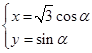 (
(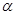 为参数)
为参数)
(I)已知在极坐标系(与直角坐标系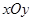 取相同的长度单位,且以原点
取相同的长度单位,且以原点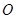 为极点,以
为极点,以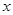 轴正半轴为极轴)中,点
轴正半轴为极轴)中,点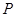 的极坐标
的极坐标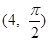 ,判断点
,判断点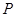 与直线
与直线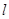 的位置关系;
的位置关系;
(II)设点 为曲线
为曲线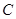 上的一个动点,求它到直线
上的一个动点,求它到直线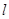 的距离的最小值.
的距离的最小值.