（本小题
满分13分）某公司是专门生产健身产品的企业，第一批产品
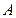上市销售40天内全部售完，该公司对第一批产品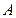上市后的市场销售进行调研，结果如图（1）、（2）所示．其中（1）的抛物线表示的是市场的日销售量与上市时间的关系；（2）的折线表示的是每件产品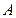的销售利润与上市时间的关系．
（1）写出市场的日销售量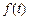
与第一批产品A上市时间t的关系式；
（2）第一批产品A上市后的第几天，这家公司日销售利润最大，最大利润是多少？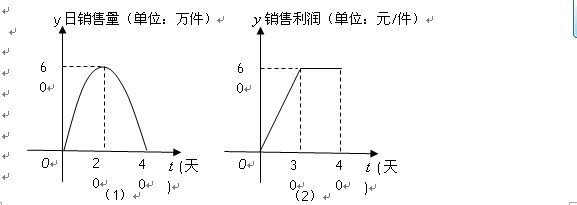
已知数列{an}为等差数列，公差d≠0,由{an}中的部分项组成的数列
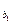a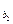
,a
,…,a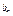
,…为等比数列，其中b1=1,b2=5,b3=17.
(1)求数列{bn}的通项公式；
(2)记Tn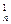=C
b1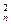+C
b2+C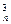
b3+…+C
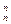bn,求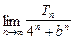
.
设等差数列{an}的前n项和为Sn,已知a3=12,S12>0,S13<0.
(1)求公差d的取值范围；
(2)指出S1、S2、…、S12中哪一个值最大，并说明理由.
已知函数f(x)在(－∞,0)∪(0,+∞)上有定义，且在(0,+∞)上是增函数，f(1)=0,又g(θ)=sin2θ－mcosθ－2m,θ∈［0,
］,设M={m|g(θ)<0,m∈R},N={m|f［g(θ)］<0},求M∩N.
某工厂拟建一座平面图(如下图)为矩形且面积为200平方米的三级污水处理池，由于地形限制，长、宽都不能超过16米，如果池外周壁建造单价为每米400元，中间两条隔墙建造单价为每米248元，池底建造单价为每平方米80元(池壁厚度忽略不计，且池无盖).
(1)写出总造价y(元)与污水处理池长x(米)的函数关系式，并指出其定义域.
(2)求污水处理池的长和宽各为多少时，污水处理池的总造价最低？并求最低总造价. 
定义在(－1，1)上的函数f(x)满足①对任意x、y∈(－1,1),都有f(x)+f(y)=f(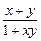
);②当x∈(－1,0)时，有f(x)>0.
求证: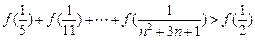
.