集合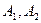 满足
满足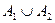 =A,则称(
=A,则称(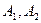 )为集合A的一种分拆,并规定:当且仅当
)为集合A的一种分拆,并规定:当且仅当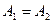 时,(
时,(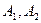 )与(
)与(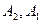 )为集合A的同一种分拆,则集合A={
)为集合A的同一种分拆,则集合A={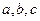 }的不同分拆种数为多少?
}的不同分拆种数为多少?
某研究机构对高三学生的记忆力x和判断力y进行统计分析,得下表数据
| x |
6 |
8 |
10 |
12 |
| y |
2 |
3 |
5 |
6 |
(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程
(2)试根据已求出的线性回归方程,预测记忆力为9的同学的判断力.
已知曲线C:
(1)当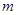 为何值时,曲线C表示圆;
为何值时,曲线C表示圆;
(2)在(1)的条件下,若曲线C与直线 交于M、N两点,且
交于M、N两点,且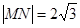 ,求
,求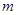 的值.
的值.
(3)在(1)的条件下,设直线 与圆
与圆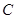 交于
交于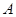 ,
, 两点,是否存在实数
两点,是否存在实数 ,使得以
,使得以 为直径的圆过原点,若存在,求出实数
为直径的圆过原点,若存在,求出实数 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB中点,D为PB中点,且△PMB为正三角形. 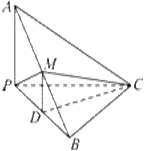
(1)求证DM∥平面APC;
(2)求证平面ABC⊥平面APC;
(3)若BC=PC=4,求二面角P-AB-C的正弦值.
已知数列 是一个等差数列且
是一个等差数列且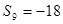 ,
, ,
,
(1)求 通项公式;
通项公式;
(2)求 的前
的前 项和
项和 的最小值.
的最小值.
风景秀美的湖畔有四棵高大的银杏树,记做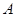 、
、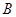 、
、 、
、 ,欲测量
,欲测量 、
、 两棵树和
两棵树和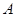 、
、 两棵树之间的距离,但湖岸部分地方围有铁丝网不能靠近,现在可以方便的测得
两棵树之间的距离,但湖岸部分地方围有铁丝网不能靠近,现在可以方便的测得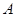 、
、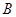 两点间的距离为
两点间的距离为 米,如图,同时也能测量出
米,如图,同时也能测量出 ,
,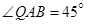 ,
, ,
, ,则
,则 、
、 两棵树和
两棵树和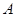 、
、 两棵树之间的距离各为多少?
两棵树之间的距离各为多少?