(本小题满分12分)已知函数f(x)=1+ (-2<x≤2).
(-2<x≤2).
(1)用分段的形式表示该函数;
(2)画出函数的图象.
(3)写出函数的值域、单调区间.
(1) 已知 ,化简
,化简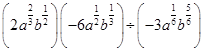 ;
;
(2) 已知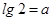 ,
,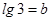 ,试用
,试用 表示
表示
已知函数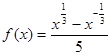 ,
, ;
;
(Ⅰ)证明 是奇函数;(Ⅱ)证明
是奇函数;(Ⅱ)证明 在(-∞,-1)上单调递增;
在(-∞,-1)上单调递增;
(Ⅲ)分别计算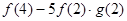 和
和 的值,由此概括出涉及函数
的值,由此概括出涉及函数 和
和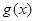 的对所有不等于零的实数
的对所有不等于零的实数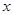 都成立的一个等式,并加以证明.
都成立的一个等式,并加以证明.
已知定义在 上的函数
上的函数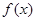 满足下列条件:1对定义域内任意
满足下列条件:1对定义域内任意 ,恒有
,恒有 ;2当
;2当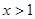 时
时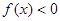 ;3
;3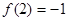 (1)求
(1)求 的值;(2)求证:函数
的值;(2)求证:函数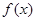 在
在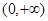 上为减函数;(3)解不等式 :
上为减函数;(3)解不等式 :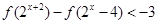
如图,在等腰梯形OABC中,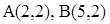 .直线
.直线 (t>0)由点O向点C移动,至点C完毕,记扫描梯形时所得直线
(t>0)由点O向点C移动,至点C完毕,记扫描梯形时所得直线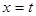 左侧的图形面积为
左侧的图形面积为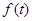 .试求
.试求 的解析式,并画出
的解析式,并画出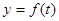 的图像.
的图像.
已知函数f(x)=Asin(ωx+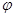 )+b(ω>0,|
)+b(ω>0,|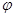 |<
|<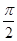 的图象的一部分如图所示。
的图象的一部分如图所示。
(1)求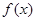 的表达式;(2)试写出
的表达式;(2)试写出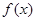 的对称抽方程;(3)求
的对称抽方程;(3)求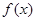 的对称中心。
的对称中心。