已知函数
(1)当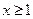 时, 证明: 不等式
时, 证明: 不等式 恒成立;
恒成立;
(2)若数列 满足
满足 ,证明数列
,证明数列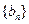 是等比数列,并求出数列
是等比数列,并求出数列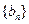 、
、 的通项公式;
的通项公式;
(3)在(2)的条件下,若 ,证明:
,证明: .
.
已知椭圆C的方程为 左、右焦点分别为F1、F2,焦距为4,点M是椭圆C上一点,满足
左、右焦点分别为F1、F2,焦距为4,点M是椭圆C上一点,满足
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点P(0,2)分别作直线PA,PB交椭圆C于A,B两点,设直线PA,PB的斜率分别为k1,k2, ,求证:直线AB过定点,并求出直线AB的斜率k的取值范围。
,求证:直线AB过定点,并求出直线AB的斜率k的取值范围。
如图。在直三棱柱ABC—A1B1C1中,AB=BC=2AA1,∠ABC=90°,M是BC中点。
(I)求证:A1B∥平面AMC1;
(II)求直线CC1与平面AMC1所成角的正弦值;
(Ⅲ)试问:在棱A1B1上是否存在点N,使AN与MC1成角60°?若存在,确定点N的位置;若不存在,请说明理由。
某校从参加某次知识竞赛的同学中,选取60名同学将其成绩(百分制,均为整数)分成6组后,得到部分频率分布直方图(如图),观察图中的信息,回答下列问题.
(Ⅰ)求分数在[70,80)内的频率,并补全这个频率分布直方图;
(Ⅱ)根据频率分布直方图,估计本次考试的平均分;
(Ⅲ)若从60名学生中随机抽取2人,抽到的学生成绩在[40,70)记0分,记[70,100]记1分,用X表示抽取结束后的总记分,求X的分布列和数学期望。
已知数列{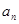 }中
}中
(I)设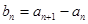 ,求证数列{
,求证数列{ }是等比数列;
}是等比数列;
(Ⅱ)求数列{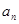 }的通项公式.
}的通项公式.
设函数 。
。
(1)求不等式 的解集;
的解集;
(2)若存在x使不等式 成立,求实数a的取值范围。
成立,求实数a的取值范围。