已知椭圆 (a>b>0)的离心率为
(a>b>0)的离心率为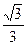 ,过右焦点F的直线
,过右焦点F的直线 与椭圆C相交于AB两点,当
与椭圆C相交于AB两点,当 斜率为1时,坐标原点O到
斜率为1时,坐标原点O到 的距离为
的距离为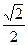
(Ⅰ)求a,b的值;
(Ⅱ)C上是否存在点P,使得当l绕F转到某一位置时,有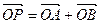 成立?
成立?
若存在,求出所有的P的坐标与l的方程;若不存在,说明理由。
已知等比数列 的前
的前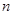 项和为
项和为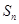 ,
,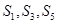 成等差数列,且
成等差数列,且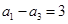
(Ⅰ)求 的通项公式
的通项公式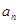 ;
;
(Ⅱ)求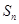 ,并求满足
,并求满足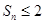 的
的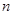 值.
值.
已知函数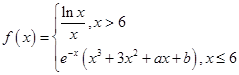 ,其中
,其中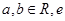 为自然对数的底数.
为自然对数的底数.
(Ⅰ)当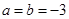 时,求函数
时,求函数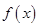 的单调区间;
的单调区间;
(Ⅱ)当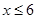 时,若函数
时,若函数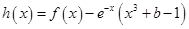 存在两个相距大于2的极值点,求实数
存在两个相距大于2的极值点,求实数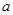 的取值范围;
的取值范围;
(Ⅲ)若函数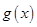 与函数
与函数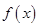 的图象关于
的图象关于 轴对称,且函数
轴对称,且函数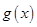 在
在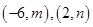 单调递减,在
单调递减,在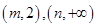 单调递增,试证明:
单调递增,试证明: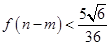 .
.
如图,已知椭圆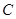 的中心在原点,其一个焦点与抛物线
的中心在原点,其一个焦点与抛物线 的焦点相同,又椭圆
的焦点相同,又椭圆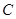 上有一点
上有一点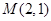 ,直线
,直线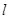 平行于
平行于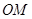 且与椭圆
且与椭圆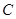 交于
交于 两点,连
两点,连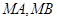
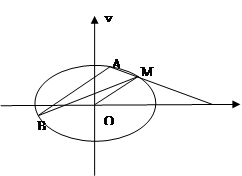
(Ⅰ)求椭圆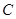 的方程;
的方程;
(Ⅱ)当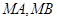 与
与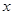 轴所构成的三角形是以
轴所构成的三角形是以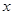 轴上所在线段为底边的等腰三角形时,求直线
轴上所在线段为底边的等腰三角形时,求直线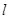 在
在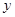 轴上截距的取值范围.
轴上截距的取值范围.
已知各项不为零的数列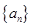 的前
的前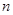 项和为
项和为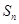 ,且满足
,且满足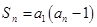 ,数列
,数列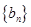 满足
满足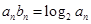 ,数列
,数列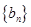 的前
的前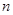 项和
项和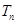
(Ⅰ)求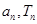
(Ⅱ)若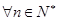 ,不等式
,不等式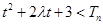 恒成立,求使关于
恒成立,求使关于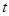 的不等式有解的充要条件.
的不等式有解的充要条件.
在如图所示的几何体中, △ABC为正三角形,AE和CD都垂直于平面ABC,且AE=AB=2,CD=1,F为BE的中点.
(Ⅰ)求证:平面DBE⊥平面ABE;
(Ⅱ)求直线BD和平面ACDE所成角的余弦值.