（本小题满分12分）如图，四棱锥P-ABCD中，PD⊥平面ABCD，PD="DC=BC=1," AB="2," AB∥DC，∠BCD=900
(1)求证：PC⊥BC
(2)求点A到平面PBC的距离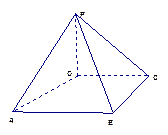
如图所示几何体是正方体
截去三棱锥
后所得，点
为
的中点.
(1) 求证：
平面
；
(2) 当正方体棱长等于
时，求三棱锥
的体积.
每年5月17日为国际电信日，某市电信公司在电信日当天对办理应用套餐的客户进行优惠，优惠方案如下：选择套餐一的客户可获得优惠200元，选择套餐二的客户可获得优惠500元，选择套餐三的客户可获得优惠300元.电信日当天参与活动的人数统计结果如图所示，现将频率视为概率.
(1) 求某人获得优惠金额不低于300元的概率；
(2) 若采用分层抽样的方式从参加活动的客户中选出6人，再从该6人中随机选出两人，求这两人获得相等优惠金额的概率.
在△
中，三个内角
、
、
所对的边分别为
、
、
，且
.
(1) 求角；
(2) 若△的面积
，
，求的值.
已知等比数列
的各项均为正数，且
，
.
(1) 求数列的通项公式；
(2) 设
，求数列
的前
项和
.
已知函数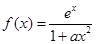
，其中
为实数，常数
.
(1) 若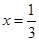
是函数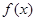
的一个极值点，求的值；
(2) 当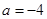
时，求函数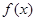的单调区间；
(3) 当取正实数时，若存在实数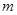
，使得关于
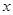的方程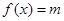
有三个实数根，求的取值范围.