已知函数 。
。
(1)讨论函数 在定义域内的最值;
在定义域内的最值;
(2)已知数列 满足
满足 。
。
① 证明对一切 且
且 ,
, ;
;
② 证明对一切 ,
, (这里
(这里 是自然对数的底数)。
是自然对数的底数)。
设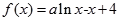 ,(
,( ),曲线
),曲线 在点
在点 处的切线垂直于
处的切线垂直于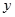 轴.
轴.
(Ⅰ) 求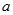 的值;
的值;
(Ⅱ) 求函数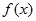 的极值。
的极值。
已知向量 ,
, ,
,
(Ⅰ)若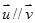 ,求实数
,求实数 的值;
的值;
(Ⅱ)若 ,求实数
,求实数 的值。
的值。
已知实数集R,集合 ,集合
,集合 ,集合
,集合 .
.
(Ⅰ)求 (C
(C ;
;
(Ⅱ)若 ,求
,求 的取值范围。
的取值范围。
已知函数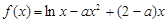 .
.
(1)讨论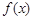 的单调性;
的单调性;
(2)设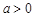 ,证明:当
,证明:当 时,
时, ;
;
(3)若函数 的图像与x轴交于A,B两点,线段AB中点的横坐标为x0,证明:
的图像与x轴交于A,B两点,线段AB中点的横坐标为x0,证明: (x0)<0.
(x0)<0.
已知平面上的线段l及点P,在l上任取一点Q,线段PQ长度的最小值称为点P到线段l的距离,记作 。
。
(1)已知点 ,线段
,线段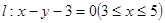 ,求
,求 ;
;
(2)设A(-1,0),B(1,0),求点集 所表示图形的面积;
所表示图形的面积;
(3)若M(0,1),O(0,0),N(2,0),画出集合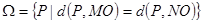 所表示的图形。
所表示的图形。