已知a=(2cosx,cos2x),b=(sinx,-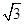 ),f(x)=a·b.
),f(x)=a·b.
(1)求f(x)的振幅、周期,并画出它在一个周期内的图象;
(2)说明它可以由函数y=sinx的图象经过怎样的变换得到.
已知函数f(x)=2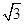 ·sin
·sin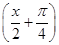 cos
cos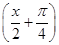 -sin(x+π).
-sin(x+π).
(1)求f(x)的最小正周期;
(2)若将f(x)的图象向右平移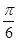 个单位,得到函数g(x)的图象,求函数g(x)在区间[0,π]上的最大值和最小值.
个单位,得到函数g(x)的图象,求函数g(x)在区间[0,π]上的最大值和最小值.
为了得到函数y=2sin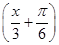 (x∈R)的图象,只需把函数y=2sinx(x∈R)的图象上所有的点经过怎样的变换得到?
(x∈R)的图象,只需把函数y=2sinx(x∈R)的图象上所有的点经过怎样的变换得到?
已知sin(3π+θ)= ,
,
求 的值.
的值.
已知在△ABC中,sinA+cosA= .
.
(1)求sinA·cosA;
(2)判断△ABC是锐角三角形还是钝角三角形;
(3)求tanA的值.