(本小题满分12分)
某工厂拟建一座平面图为矩形且面积为200平方米的三级污水处理池(平面图如图)。由于地形限制,长、宽都不能超过16米。如果池外圈四周壁造价为每平方米400元,中间两条隔墙造价为每平方米248元,池底造价为每平方米80元,池壁的厚度不计。试设计污水处理池的长和宽,使总造价最低,并求出最低总造价。(池深用h 表示)
(本小题满分12分)如图四棱锥 的底面是正方形,
的底面是正方形,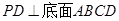 ,点E在棱PB上,O为AC与BD的交点。
,点E在棱PB上,O为AC与BD的交点。
(1)求证:平面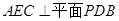 ;
;
( 2)当E为PB中点时,求证:
2)当E为PB中点时,求证: //平面PDA,
//平面PDA, //平面PDC。
//平面PDC。
(3)当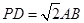 且E为PB的中点时,求
且E为PB的中点时,求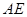 与平面
与平面 所成的角的大小。
所成的角的大小。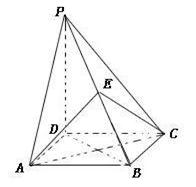
(本小题满分12分)设 ,其中
,其中 为正实数
为正实数
(1)当
 时,求
时,求 的极值点;
的极值点;
(2)若 为
为 上的单调函数,求
上的单调函数,求 的取值范围。
的取值范围。
已知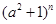 展开式中的各项系数之和等于
展开式中的各项系数之和等于 的展开式的常数项,而
的展开式的常数项,而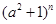 的展开式的系数最大的项等于54,求
的展开式的系数最大的项等于54,求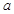 的值.
的值.
.已知等差数列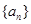 中,公差
中,公差 ,其前
,其前 项和为
项和为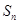 ,且满足
,且满足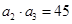 ,
, .
.
(1)求数列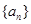 的通项公式;
的通项公式;
(2)设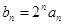 (
(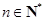 ),求数列
),求数列 的前
的前 项和
项和 ;
;
(3)设 ,试比较
,试比较 与
与 的大小.
的大小.
已知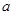 为实数,函数
为实数,函数 .
.
(1)若 ,求
,求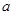 的值及曲线
的值及曲线 在
在 处的切线方程;
处的切线方程;
(2)求 在区间
在区间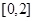 上的最大值.
上的最大值.