(本小题满分12分)已知函数 的定义域为(0,+∞),且满足对任意的
的定义域为(0,+∞),且满足对任意的 >0,y>0,
>0,y>0, ,
, .当
.当 >1时,
>1时, >0.
>0.
(1)求 的值
的值
(2)判断 的单调性,并加以证明
的单调性,并加以证明
(3)解不等式 .
.
(本小题12分)
我国是水资源匮乏的国家为鼓励节约用水,某市打算出台一项水费政策措施,规定:每一季度每人用水量不超过5吨时,每吨水费收基本价1.3元;若超过5吨而不超过6吨时,超过部分水费加收200%;若超过6吨而不超过7吨时,超过部分的水费加收400%,如果某人本季度实际用水量为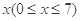 吨,
吨,
应交水费为 .
.
(1)求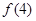 、
、 、
、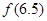 的值;
的值;
(2)试求出函数 的解析式.
的解析式.
(本小题12分)
设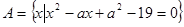 ,
, ,
,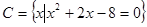
(1)若 ,求
,求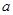 的值;
的值;
(2)若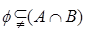 且
且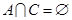 ,求
,求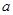 的值;
的值;
(3)若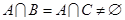 ,求
,求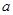 的值.
的值.
(本小题12分)
已知函数 ,
,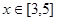 ,
,
⑴判断函数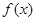 的单调性,并证明;
的单调性,并证明;
⑵求函数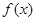 的最大值和最小值.
的最大值和最小值.
(本小题12分)
设集合 ,
, .若
.若 ,求实数
,求实数 的值组成的集合.
的值组成的集合.
(本小题10分)
若 ,求实数
,求实数 的值.
的值.