(本题满分12分)
投掷飞碟的游戏中,飞碟投入红袋记2分,投入蓝袋记1分,未投入袋记0分.现知某人在以前投掷1000次的试验中,有500次入红袋,250次入蓝袋,其余不能入袋
(1)求该人在4次投掷中恰有三次投入红袋的概率;
(2) 求该人两次投掷后得分 的分布列和数学期望.
的分布列和数学期望.
已知函数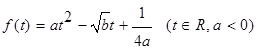 的最大值为正实数,集合
的最大值为正实数,集合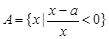 ,集合
,集合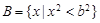 。
。
(1)求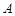 和
和 ;
;
(2)定义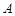 与
与 的差集:
的差集: 且
且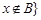 。
。
设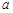 ,
, ,
,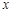 均为整数,且
均为整数,且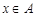 。
。 为
为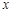 取自
取自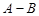 的概率,
的概率,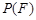 为
为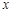 取自
取自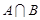 的概率,写出
的概率,写出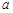 与
与 的二组值,使
的二组值,使 ,
, 。
。
(3)若函数 中,
中, ,
, 是(2)中
是(2)中 较大的一组,试写出
较大的一组,试写出 在区间[
在区间[ ,n]上的最大值函数
,n]上的最大值函数 的表达式。
的表达式。
已知点列B1(1,y1)、B2(2,y2)、…、Bn(n,yn)(n∈N)顺次为一次函数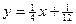 图象上的点,点列A1(x1,0)、A2(x2,0)、…、An(xn,0)(n∈N)顺次为x轴正半轴上的点,其中x1=a(0<a<1),对于任意n∈N,点An、Bn、An+1构成以
图象上的点,点列A1(x1,0)、A2(x2,0)、…、An(xn,0)(n∈N)顺次为x轴正半轴上的点,其中x1=a(0<a<1),对于任意n∈N,点An、Bn、An+1构成以
Bn为顶点的等腰三角形。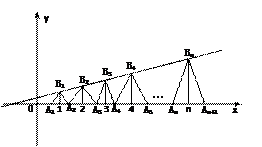
⑴求{yn}的通项公式,且证明{yn}是等差数列;
⑵试判断xn+2-xn是否为同一常数(不必证明),并求出数列{xn}的通项公式;
⑶在上述等腰三角形AnBnAn+1中,是否存在直角三角形?若有,求出此时a值;
若不存在, 请说明理由。
已知 之间满足
之间满足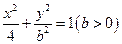
(1)方程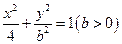 表示的曲线经过一点
表示的曲线经过一点 ,求b的值
,求b的值
(2)动点(x,y)在曲线 (b>0)上变化,求x2+2y的最大值;
(b>0)上变化,求x2+2y的最大值;
(3)由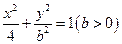 能否确定一个函数关系式
能否确定一个函数关系式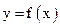 ,如能,求解析式;如不能,再加什么条件就可使
,如能,求解析式;如不能,再加什么条件就可使 之间建立函数关系,并求出解析式。
之间建立函数关系,并求出解析式。
已知等比数列{an}的前n项和为Sn.
(Ⅰ)若Sm,Sm+2,Sm+1成等差数列,证明am,am+2,am+1成等差数列;
(Ⅱ)写出(Ⅰ)的逆命题,判断它的真伪,并给出证明.
设M是由满足下列条件的函数 构成的集合:“①方程
构成的集合:“①方程
 有实数根;②函数
有实数根;②函数 的导数
的导数 满足
满足 .”
.”
(I)判断函数 是否是集合M中的元素,并说明理由;
是否是集合M中的元素,并说明理由;
(II)集合M中的元素 具有下面的性质:若
具有下面的性质:若 的定义域为D,则对于任意
的定义域为D,则对于任意
[m,n] D,都存在
D,都存在
 [m,n],使得等式
[m,n],使得等式 成立”,
成立”,
试用这一性质证明:方程 只有一个实数根;
只有一个实数根;
(III)设 是方程
是方程 的实数根,求证:对于
的实数根,求证:对于 定义域中任意的
定义域中任意的 .
.