设
分别是椭圆C：
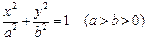的左右焦点，
（1）设椭圆C上的点
到两点距离之和等于4，写出椭圆C的方程和焦点坐标。
（2）设K是（1）中所得椭圆上的动点，求线段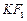
的中点B的轨迹方程。
（3
）设点P是椭圆C 上的任意一点，过原点的直线L与椭圆相交于M，N两点，当直线PM ，PN的斜率都存在，并记为
试探究
的值是否与点P及直线L有关，并证明你的结论。
已知
（1）当a=1时，求
的单调区间
（2）是否存在实数a，使的极大值为3？若存在，求出a的值，若不存在，说明理由．
|
已知函数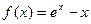
（
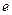为自然对数的底数）
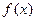的最小值
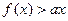的解集为P，且
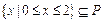，求实数a的取值范围
已知函数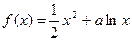
（a∈R）．(1)若
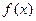在[1，e]上是增函数，求a的取值范围（2）若a=1,a≤x≤e,证明：<
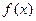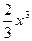
已知函数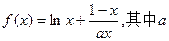
为大于零的常数。
（1）若函数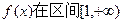
内单调递增，求a的取值范围
（2）求函数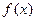
在区间[1，2]上的最小值。
已知函数f(x)=
x3-2ax2+3x(x∈R)．
（1）若a=1,点P为曲线y=f(x)上的一个动点，求以点P为切点的切线斜率取最小值时的切线方程
（2）若函数y=f(x)在（0，+∞）上为单调增函数，试求满足条件的最大整数a．