已知函数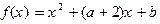 满足
满足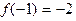 ;
;
①若方程 有唯一的解,求实数
有唯一的解,求实数 的值;
的值;
②若函数 的定义域为R,求实数
的定义域为R,求实数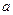 的取值范围.
的取值范围.
题号:04
“矩阵与变换和坐标系与参数方程”模块(10分)
在极坐标系中,极点为A,已知“葫芦”型封闭曲线 由圆弧ACB和圆弧BDA组成.已知
由圆弧ACB和圆弧BDA组成.已知
(1)求圆弧ACB和圆弧BDA的极坐标方程;
(2)求曲线 围成的区域面积.
围成的区域面积.
数学自选模块
题号:03
“数学史与不等式选讲”模块
已知函数 ,且
,且 ,对于定义域内的任意实数
,对于定义域内的任意实数 (1)设
(1)设 时,S取得最小值,求a,b的值;(2)在(1)的条件下,证明:对任意
时,S取得最小值,求a,b的值;(2)在(1)的条件下,证明:对任意 成立.
成立.
(本小题满分15分)设 ,函数
,函数 ,
, .
.
(1)当 时,比较
时,比较 与
与 的大小;
的大小;
(2)若存在实数 ,使函数
,使函数 的图象总在函数
的图象总在函数 的图象的上方,求
的图象的上方,求 的取值集合.
的取值集合.
(本题满分15分) 已知抛物线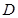 的顶点是椭圆
的顶点是椭圆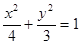 的中心,焦点与该椭圆的右焦点重合.
的中心,焦点与该椭圆的右焦点重合.
(1)求抛物线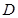 的方程;
的方程;
(2)已知动直线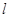 过点
过点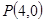 ,交抛物线
,交抛物线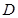 于
于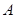 、
、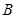 两点.
两点.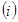 若直线
若直线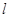 的斜率为1,求
的斜率为1,求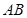 的长;
的长;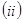 是否存在垂直于
是否存在垂直于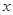 轴的直线
轴的直线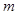 被以
被以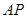 为直径的圆
为直径的圆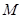 所截得的弦长恒为定值?如果存在,求出
所截得的弦长恒为定值?如果存在,求出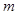 的方程;如果不存在,说明理由.
的方程;如果不存在,说明理由.
(本小题满分14分)如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD//BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC= AD=1,CD=
AD=1,CD= .
.
(1)求证:平面PQB⊥平面PAD;
(2)若二面角M-BQ-C为30°,设PM=tMC,
试确定t的值