设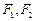 分别是椭圆
分别是椭圆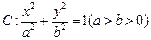 的左、右焦点,过
的左、右焦点,过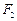 的直线
的直线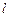 与椭圆
与椭圆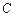 相交于A,B两点,直线
相交于A,B两点,直线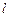 的倾斜角为
的倾斜角为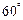 ,
,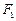 到直线
到直线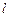 的距离为
的距离为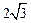 .
.
(1)求椭圆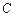 的焦距;
的焦距;
(2)如果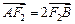 ,求椭圆
,求椭圆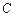 的方程.
的方程.
(本小题满分12分)已知数列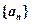 、
、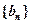 的前n项和分别为
的前n项和分别为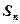 、
、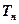 ,且满足
,且满足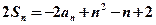 ,
,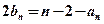 。
。
(Ⅰ)求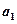 、
、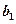 的值,并证明数列
的值,并证明数列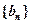 是等比数列;
是等比数列;
(Ⅱ)试确定实数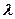 的值,使数列
的值,使数列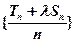 是等差数列。
是等差数列。
(本题满分12分)在四棱锥P—ABCD中,底面ABCD是a的正方形,PA⊥平面ABCD,且PA=2AB
(Ⅰ)求证:平面PAC⊥平面PBD;
(Ⅱ)求二面角B—PC—D的余弦值.
(本小题满分12分)在一个选拔项目中,每个选手都需要进行4轮考核,每轮设有一个问题,能正确回答者进入下一轮考核,否则被淘汰。已知某选手能正确回答第一、二、三、四轮问题的概率分别为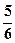 、
、 、
、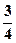 、
、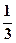 ,且各轮问题能否正确回答互不影响。
,且各轮问题能否正确回答互不影响。
(Ⅰ)求该选手进入第三轮才被淘汰的概率;
(Ⅱ)求该选手至多进入第三轮考核的概率;
(Ⅲ)该选手在选拔过程中回答过的问题个数记为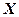 ,求随机变量
,求随机变量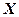 的分布列和期望。
的分布列和期望。
(本题满分10分)若向量 ,其中
,其中 ,设
,设
函数 ,其周期为
,其周期为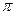 ,且
,且 是它的一条对称轴。
是它的一条对称轴。
(1)求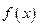 的解析式;
的解析式;
(2)当 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数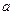 的取值范围。
的取值范围。
(本题满分12分)
已知 (m为常数,且m>0)有极大值
(m为常数,且m>0)有极大值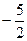 ,
,
(Ⅰ)求m的值;
(Ⅱ)求曲线 的斜率为2的切线方程.
的斜率为2的切线方程.