(本小题满分12分)
如图,四棱锥P—ABCD的底面ABCD是边长为2的菱形,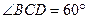 ,E是CD的中点,PA
,E是CD的中点,PA 底面ABCD,PA=4
底面ABCD,PA=4
(1)证明:若F是棱PB的中点,求证:EF//平面PAD;
(2)求平面PAD和平面PBE所成二面角(锐角)的大小。
(本小题满分10分)已知直线 的参数方程为
的参数方程为 (其中
(其中 为参数),曲线
为参数),曲线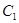 :
: ,以坐标原点为极点,
,以坐标原点为极点, 轴正半轴为极轴,建立极坐标系,两种坐标系中取相同长度单位。
轴正半轴为极轴,建立极坐标系,两种坐标系中取相同长度单位。
(1)求直线 的普通方程及曲线
的普通方程及曲线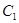 的直角坐标方程;
的直角坐标方程;
(2)在曲线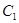 上是否存在一点
上是否存在一点 ,使点
,使点 到直线
到直线 的距离最大?若存在,求出距离最大值及点
的距离最大?若存在,求出距离最大值及点 .若不存在,请说明理由。
.若不存在,请说明理由。
(本小题满分10分)如图, 的半径
的半径 垂直于直径
垂直于直径 ,
, 为
为 上一点,
上一点, 的延长线交
的延长线交 于
于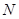 ,过
,过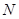 点的切线交
点的切线交 的延长线于
的延长线于 。
。
(1)求证: ;
;
(2)若 的半径为
的半径为 ,
, .求:
.求: 的长。
的长。
(本小题满分12分) 已知函数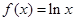 .
.
(1)求函数 的最大值;
的最大值;
(2)求证:
(3)当 时,求证:
时,求证: .
.
(本小题满分12分)过椭圆 的右焦点
的右焦点 作斜率
作斜率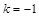 的直线交椭圆于
的直线交椭圆于 两点,且
两点,且 与
与 共线.
共线.
(1)求椭圆的离心率;
(2)设 为椭圆上任意一点,且
为椭圆上任意一点,且 ,证明:
,证明: 为定值。
为定值。
(本小题满分12分)如图,正方形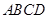 所在平面与等腰三角形
所在平面与等腰三角形 所在平面相交于
所在平面相交于
 平面
平面 .
.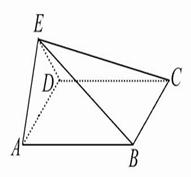
(1)求证: 平面
平面 ;
;
(2)设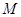 是线段
是线段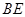 上一点,当直线
上一点,当直线 与平面
与平面 所成角的正弦值为
所成角的正弦值为 时,试确定点
时,试确定点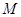 的位置.
的位置.