已知直线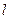 过定点
过定点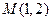 ,且与抛物线
,且与抛物线 交于
交于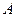 、
、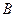 两点,抛物线在
两点,抛物线在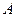 、
、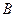 两点处的切线的相交于点
两点处的切线的相交于点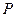 .
.
(I)求点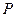 的轨迹方程;
的轨迹方程;
(II)求三角形 面积的最小值.
面积的最小值.
已知函数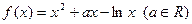 .
.
(I)若函数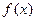 在
在 上是减函数,求实数
上是减函数,求实数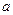 的取值范围;
的取值范围;
(II)令 ,是否存在实数
,是否存在实数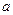 ,使得当
,使得当 时,函数
时,函数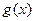 的最小值是
的最小值是 ,若存在,求出实数
,若存在,求出实数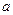 的值,若不存在,说明理由?
的值,若不存在,说明理由?
(III)当 时,证明:
时,证明: .
.
已知函数 ,
,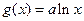
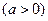 ,点
,点 是函数
是函数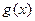 图象上任意一点,直线
图象上任意一点,直线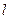 为函数
为函数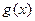 的图象在
的图象在 处的切线.
处的切线.
(I)求直线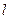 的方程;
的方程;
(II)若直线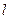 与
与 的图象相切,求
的图象相切,求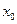 和
和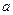 的取值范围.
的取值范围.
已知椭圆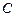 的方程是
的方程是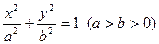 ,椭圆的左顶点为
,椭圆的左顶点为 ,离心率
,离心率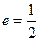 ,倾斜角为
,倾斜角为 的直线
的直线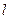 与椭圆交于
与椭圆交于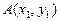 、
、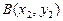 两点.
两点.
(Ⅰ)求椭圆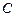 的方程;
的方程;
(Ⅱ)设向量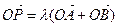 (
(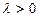 ),若点
),若点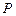 在椭圆
在椭圆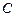 上,求
上,求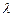 的取值范围.
的取值范围.
已知 两地的距离是120km.假设汽油的价格是6元/升,以
两地的距离是120km.假设汽油的价格是6元/升,以 km/h(其中
km/h(其中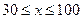 )速度行驶时,汽车的耗油率为
)速度行驶时,汽车的耗油率为 L/h,司机每小时的工资是28元.那么最经济的车速是多少?如不考虑其他费用,这次行车的总费用是多少?
L/h,司机每小时的工资是28元.那么最经济的车速是多少?如不考虑其他费用,这次行车的总费用是多少?