(本题14分)已知函数 ,
, 。
。
(1)当t=8时,求函数 的单调区间;
的单调区间;
(2)求证:当 时,
时, 对任意正实数
对任意正实数 都成立;
都成立;
(3)若存在正实数 ,使得
,使得 对任意的正实数
对任意的正实数 都成立,请直接写出满足这样条件的一个
都成立,请直接写出满足这样条件的一个 的值(不必给出求解过程)
的值(不必给出求解过程)
已知函数 时取最大值2。
时取最大值2。 是集合
是集合 中的任意两个元素,
中的任意两个元素, 的最小值为
的最小值为 。
。
(1)求a、b的值;
(2)若 的值。
的值。
已知圆C:x2+y2+2x-4y+3=0,若圆C的切线在x轴和y轴上的截距绝对值相等,求切线方程.
实数a,b,c满足条件3(a2+b2)=4c2(c≠0).
(1)求证:直线ax+by+c=0与圆x2+y2=1交于不同的两点P、Q;
(2)求弦PQ的长.
已知圆的方程是x2+y2=2,直线y=x+b,当b为何值时,圆与直线有两个公共点?
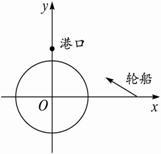
一艘轮船沿直线返回港口的途中,接到气象台的台风预报,台风中心位于轮船正西70 km处,受影响的范围是半径为30 km的圆形区域,已知港口位于台风中心正北40 km处,如果这艘轮船不改变航线,那么它是否会受到台风的影响?