（本小题满分12分）
已知集合
（1）求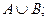
（2）若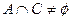
,求a的取值范围.
已知函数f(x)＝
，x∈(1，＋∞)．
(1)求函数f(x)的单调区间；
(2)函数f(x)在区间[2，＋∞)上是否存在最小值，若存在，求出最小值，若不存在，请说明理由．
已知函数f(x)＝axln x图象上点(e，f(e))处的切线与直线y＝2x平行，g(x)＝x2－tx－2.
(1)求函数f(x)的解析式；
(2)求函数f(x)在[n，n＋2](n>0)上的最小值；
(3)对一切x∈(0，e]，3f(x)≥g(x)恒成立，求实数t的取值范围．
已知函数f(x)＝ax＋ln x，g(x)＝ex.
(1)当a≤0时，求f(x)的单调区间；
(2)若不等式g(x)<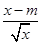 
有解，求实数m的取值范围．
已知函数f(x)＝－aln x＋
＋x(a≠0)，
(1)若曲线y＝f(x)在点(1，f(1))处的切线与直线x－2y＝0垂直，求实数a的值；
(2)讨论函数f(x)的单调性．
已知椭圆C：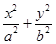
＝1(a>b>0)的离心率与等轴双曲线的离心率互为倒数关系，直线l：x－y＋
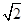＝0与以原点为圆心， 以椭圆C的短半轴长为半径的圆相切．
(1)求椭圆C的方程；
(2)设M是椭圆的上顶点，过点M分别作直线MA，MB交椭圆于A，B两点，设两直线的斜率分别为k1，k2，且k1＋k2＝4，证明：直线AB过定点
.