(本小题满分13分)设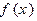 是定义在
是定义在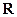 上的函数,对任意实数
上的函数,对任意实数 、
、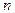 ,都有
,都有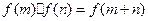 ,且当
,且当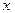 <0时,
<0时,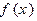 >1.
>1.
(1)证明:① ;
;
②当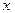 >0时,0<
>0时,0<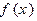 <1;
<1;
③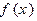 是
是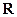 上的减函数;
上的减函数;
(2)设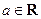 ,试解关于
,试解关于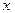 的不等式
的不等式 ;
;
选修4-2:矩阵与变换已知矩阵 ,向量
,向量 ,
,
(Ⅰ)求矩阵A的特征值和对应的特征向量;
(Ⅱ)求向量 ,使得
,使得 .
.
.已知函数
(Ⅰ)当 时,求
时,求 的值域
的值域
(Ⅱ)设 ,若
,若 在
在 恒成立,求实数a的取值范围
恒成立,求实数a的取值范围
(III)设 ,若
,若 在
在 上的所有极值点按从小到大排成一列
上的所有极值点按从小到大排成一列 ,
,
求证:
.(本小题满分13分)
以椭圆 :
: 的中心
的中心 为圆心,
为圆心, 为半径的圆称为该椭圆的“准圆”.设椭圆
为半径的圆称为该椭圆的“准圆”.设椭圆 的左顶点为
的左顶点为 ,左焦点为
,左焦点为 ,上顶点为
,上顶点为 ,且满足
,且满足 ,
, .
.
(Ⅰ)求椭圆 及其“准圆”的方程;
及其“准圆”的方程;
(Ⅱ)若椭圆 的“准圆”的一条弦
的“准圆”的一条弦 (不与坐标轴垂直)与椭圆
(不与坐标轴垂直)与椭圆 交于
交于 、
、 两点,试证明:当
两点,试证明:当 时,试问弦
时,试问弦 的长是否为定值,若是,求出该定值;若不是,请说明理由.
的长是否为定值,若是,求出该定值;若不是,请说明理由.
.(本小题满分13分)
已知数列 是各项均不为
是各项均不为 的等差数列,公差为
的等差数列,公差为 ,
, 为其前
为其前 项和.向量
项和.向量 、
、 满足
满足 ,
, .数列
.数列 满足
满足 ,
, 为数列
为数列 的前n项和.
的前n项和.
(Ⅰ)求 、
、 和
和 ;
;
(Ⅱ)若对任意的 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(本小题满分13分)
由于当前学生课业负担较重,造成青少年视力普遍下降,现从某中学随机抽取16名学生,经校医用对数视力表检査得到每个学生的视力状况的茎叶图(以小数点前的一位数字为茎,小数点后的一位数字为叶)如右:
(Ⅰ)若视力测试结果不低于5.0,则称为“好视力”,求校医从这16人中随机选取3人,至多有1人是“好视力”的概率;
(Ⅱ)以这16人的样本数据来估计整个学校的总体数据,若从该校(人数很多)任选3人,记 表示抽到“好视力”学生的人数,求
表示抽到“好视力”学生的人数,求 的分布列及数学期望.
的分布列及数学期望.