探究函数 ,
,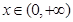 的最小值,并确定取得最小值时
的最小值,并确定取得最小值时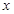 的值,列表如下:
的值,列表如下:
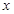 |
… |
0.5 |
1 |
1.5 |
1.7 |
1.9 |
2 |
2.1 |
2.2 |
2.3 |
3 |
4 |
5 |
7 |
… |
 |
… |
8.5 |
5 |
4.17 |
4.05 |
4.005 |
4 |
4.005 |
4.102 |
4.24 |
4.3 |
5 |
5.8 |
7.57 |
… |
请观察表中 值随
值随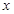 值变化的特点,完成下列问题:
值变化的特点,完成下列问题:
(1) 当 时,
时, 在区间
在区间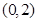 上递减,在区间 上递增;
上递减,在区间 上递增;
所以, = 时,
= 时,  取到最小值为 ;
取到最小值为 ;
(2) 由此可推断,当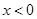 时,
时, 有最 值为 ,此时
有最 值为 ,此时 = ;
= ;
(3) 证明: 函数 在区间
在区间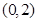 上递减;
上递减;
(4) 若方程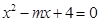 在
在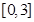 内有两个不相等的实数根,求实数
内有两个不相等的实数根,求实数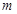 的取值范围。
的取值范围。
(1)点M到点F(2,0)的距离比它到直线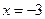 的距离小1,求点M满足的方程。
的距离小1,求点M满足的方程。
(2)曲线上点M(x,y)到定点F(2,0)的距离和它到定直线x=8的距离比是常数2,求曲线方程。
已知动圆C过点A(-2,0),且与圆M:(x-2)2+x2=64相内切
(1)求动圆C的圆心的轨迹方程;
(2)设直线l: y=kx+m(其中k,m∈Z)与(1)所求轨迹交于不同两点B,D,与双曲线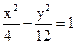 交于不同两点E
交于不同两点E ,F,问是否存在直线l,使得向量
,F,问是否存在直线l,使得向量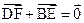 ,若存在,指出这样的直线有多少条?若不存在,请说明理由.
,若存在,指出这样的直线有多少条?若不存在,请说明理由.
设椭圆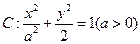 的左右焦点分别为
的左右焦点分别为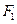 、
、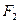 ,
, 是椭圆
是椭圆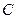 上的一点,且
上的一点,且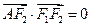 ,坐标原点
,坐标原点 到
到 直线
直线 的距离为
的距离为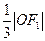 .
.
(1)求椭圆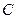 的方程;
的方程;
(2) 设 是椭圆
是椭圆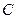 上的一点,过点
上的一点,过点 的直线
的直线 交
交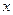 轴于点
轴于点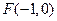 ,交
,交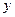 轴于点
轴于点 ,若
,若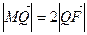 ,求直线
,求直线 的斜率.
的斜率.
动点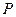 的轨迹
的轨迹 的方程为
的方程为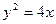 ,过焦点
,过焦点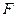 的直线
的直线 与
与 相交于
相交于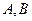 两点,
两点, 为坐标原点。(1)求
为坐标原点。(1)求 的值;
的值;
(2)设 ,当三角形
,当三角形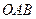 的面积
的面积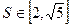 时,求
时,求 的取值范围.
的取值范围.
过双曲线 的右焦点F作倾斜角为的直线交双曲线于A、B两点,求线段AB的中点C到焦点F的距离
的右焦点F作倾斜角为的直线交双曲线于A、B两点,求线段AB的中点C到焦点F的距离