为了了解中学生的体能情况,抽取了某校一个年级的部分学生进行一次跳绳次数测试,将所得的数据 整理后,画出频率分布直方图,如下图所示,已知图中从左到右前三个小组的频率分别为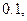
 ,
,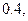 第一小组的频数为5
第一小组的频数为5
(1)求第四小组的频率;
(2)参加这次测试的学生数是多少?
(3)若次数在60次以上(含60次)为达标,试求该年级学生跳绳测试的达标率是多少?
(4)利用直方图估计该年级学生此次跳绳次数的平均值。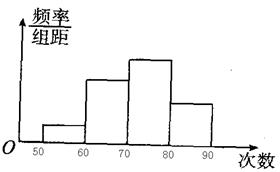
(本小题满分12分)已知数列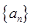 的前n项和
的前n项和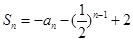 (n为正整数)。
(n为正整数)。
(1)令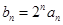 ,求证数列
,求证数列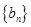 是等差数列,并求数列
是等差数列,并求数列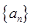 的通项公式;
的通项公式;
(2)令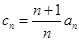 ,求数列
,求数列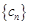 的前
的前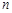 项和
项和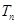 。
。
(本小题满分12分)已知命题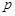 :抛物线
:抛物线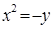 与直线
与直线 有两个不同交点;命题
有两个不同交点;命题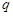 :函数
:函数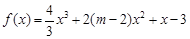 在
在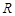 上单调递增;若
上单调递增;若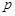 或
或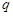 为真,
为真,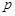 且
且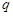 为假,求实数
为假,求实数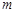 的取值范围。
的取值范围。
(本小题满分10分)若极坐标系的极点与直角坐标系的原点重合,极轴与直角坐标系的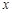 轴的正半轴重合.
轴的正半轴重合.
直线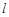 的参数方程是
的参数方程是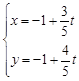 (
(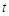 为参数),曲线
为参数),曲线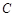 的极坐标方程为
的极坐标方程为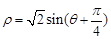 .
.
(1)求曲线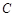 的直角坐标方程;
的直角坐标方程;
(2)设直线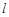 与曲线
与曲线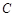 相交于
相交于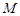 ,
,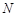 两点,求M,N两点间的距离.
两点,求M,N两点间的距离.
(本小题14分)已知点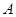 ,
,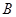 的坐标分别为
的坐标分别为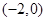 ,
,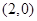 .直线
.直线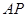 ,
,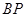 相交于点
相交于点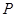 ,且它们的斜率之积是
,且它们的斜率之积是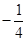 ,记动点
,记动点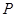 的轨迹为曲线
的轨迹为曲线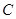 .
.
(1)求曲线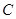 的方程;
的方程;
(2)设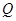 是曲线
是曲线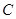 上的动点,直线
上的动点,直线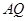 ,
,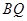 分别交直线
分别交直线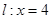 于点
于点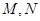 ,线段
,线段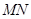 的中点为
的中点为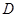 ,求直线
,求直线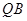 与直线
与直线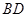 的斜率之积的取值范围;
的斜率之积的取值范围;
(3)在(2)的条件下,记直线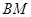 与
与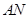 的交点为
的交点为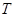 ,试探究点
,试探究点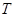 与曲线
与曲线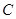 的位置关系,并说明理由.
的位置关系,并说明理由.
(本小题13分)已知抛物线的顶点在坐标原点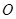 ,焦点
,焦点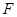 在
在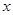 轴上,抛物线上的点
轴上,抛物线上的点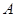 到
到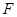 的距离为2,且
的距离为2,且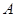 的横坐标为1.直线
的横坐标为1.直线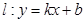 与抛物线交于
与抛物线交于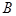 ,
,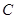 两点.
两点.
(1)求抛物线的方程;
(2)当直线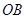 ,
,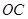 的倾斜角之和为
的倾斜角之和为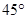 时,证明直线
时,证明直线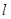 过定点.
过定点.