某种产品的广告费支出 (单位:百万元)与销售额
(单位:百万元)与销售额 (单位:百万元)之间有如下对应数据
(单位:百万元)之间有如下对应数据
 |
2 |
4 |
5 |
6 |
8 |
 |
30 |
40 |
60 |
50 |
70 |
(1)画出散点图;
(2)求线性回归方程;
(公式: )
)
(3)预测当广告费支出为7百万元时的销售额。
在平面直角坐标系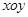 中,已知曲线
中,已知曲线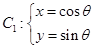 (θ为参数),将
(θ为参数),将 上的所有点的横坐标、纵坐标分别伸长为原来的
上的所有点的横坐标、纵坐标分别伸长为原来的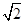 和2倍后得到曲线
和2倍后得到曲线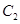 ,以平面直角坐标系
,以平面直角坐标系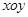 的原点
的原点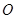 为极点,
为极点,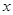 轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线
轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线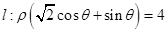 .
.
(1)试写出曲线 的极坐标方程与曲线
的极坐标方程与曲线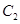 的参数方程;
的参数方程;
(2)在曲线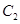 上求一点
上求一点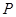 ,使点
,使点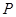 到直线
到直线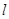 的距离最小,并求此最小值.
的距离最小,并求此最小值.
已知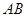 为半圆
为半圆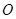 的直径,
的直径,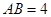 ,
, 为半圆上一点,过点圆的切线
为半圆上一点,过点圆的切线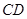 ,过
,过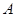 点作
点作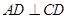 于
于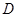 ,交半圆于点
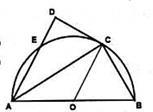
,交半圆于点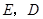 .
.
(1)证明: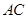 平分
平分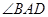 ;
;
(2)求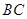 的长.
的长.
设函数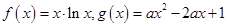 .
.
(1)求函数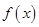 的单调区间;
的单调区间;
(2)若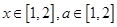 ,求证:
,求证: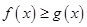 .
.
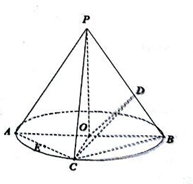
在如图所示的圆锥中,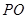 是圆锥的高,
是圆锥的高,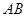 是底面圆的直径,点
是底面圆的直径,点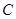 是弧
是弧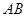 的中点,
的中点,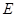 是线段
是线段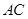 的中点,
的中点,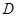 是线段
是线段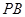 上一点,且
上一点,且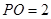 ,
,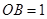 .
.
(1)若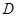 为
为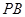 的中点,试在
的中点,试在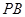 上确定一点
上确定一点 ,使得
,使得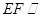 面
面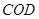 ,并说明理由;
,并说明理由;
(2)若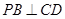 ,求直线
,求直线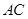 与面
与面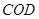 所成角
所成角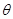 的正弦值.
的正弦值.
已知数列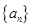 满足
满足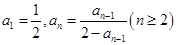 .
.
(1)求证: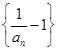 为等比数列,并求出
为等比数列,并求出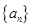 的通项公式;
的通项公式;
(2)若 ,求
,求 的前n项和
的前n项和 .
.