(本小题满分14分)设数列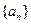 的前
的前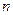 项和为
项和为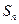 ,已知
,已知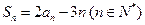 .
.
(1)求数列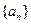 的通项公式
的通项公式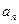 ;
;
(2)问数列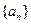 中是否存在某三项,它们可以构成一个等差数列?若存在,请求出一组适合条件的项;若不存在,请说明理由.
中是否存在某三项,它们可以构成一个等差数列?若存在,请求出一组适合条件的项;若不存在,请说明理由.
(本小题满分15分)
已知函数 .
.
(1)若 ,求函数
,求函数 在区间
在区间 的值域;
的值域;
(2)若函数 在
在 上为增函数,求
上为增函数,求 的取值范围.
的取值范围.
(本小题满分14分)
袋中装有黑球和白球共7个,从中任取1个球是白球的概率为 .现有甲、乙两人从袋中轮流摸取1球,取后不放回:甲先取,乙后取,然后甲再取……,直到两人中有一人取到白球时即终止.每个球在每一次被取出的机会是等可能的.
.现有甲、乙两人从袋中轮流摸取1球,取后不放回:甲先取,乙后取,然后甲再取……,直到两人中有一人取到白球时即终止.每个球在每一次被取出的机会是等可能的.
(1)求取球2次终止的概率;
(2)求甲取到白球的概率.
(本小题满分14分)
已知定义域为 的函数
的函数 是偶函数,当
是偶函数,当 时,
时, .
.
(1)求 的解析式;
的解析式;
(2)证明方程 在区间
在区间 上有解
上有解
(本小题满分14分)
某地区在高一年级学完《数学必修1》后进行评估测试.现从所有参加测试的全体学生中随机抽取500名学生的试卷进行统计分析,就学生的成绩制成频率分布直方图(如图).
(1)在这500名学生中,成绩不低于80分的有多少人?
(2)设成绩不低于60分为合格,求这次评估测试的合格率;
(3)估计这次评估测试的平均分.
(本小题满分12分)
已知 ,点
,点 满足
满足 ,记点
,记点 的轨迹
的轨迹 为
为 .
.
(Ⅰ)求轨迹 的方程;
的方程;
(Ⅱ)过点F2(1 ,0)作直线l与轨迹
,0)作直线l与轨迹 交于不同的两点A、B,设
交于不同的两点A、B,设
 ,若
,若 的取值范围
的取值范围