已知函数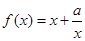 (
(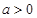 ).
).
(1)证明:当 时,
时, 在
在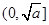 上是减函数,在
上是减函数,在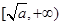 上是增函数,并写出当
上是增函数,并写出当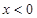 时
时 的单调区间;
的单调区间;
(2)已知函数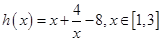 ,函数
,函数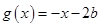 ,若对任意
,若对任意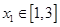 ,总存在
,总存在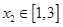 ,使得
,使得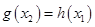 成立,求实数
成立,求实数 的取值范围.
的取值范围.
(本小题满分16分)已知函数 .(Ⅰ)当
.(Ⅰ)当 时,求证:函数
时,求证:函数 在
在 上单调递增;(Ⅱ)若函数
上单调递增;(Ⅱ)若函数 有三个零点,求
有三个零点,求 的值;
的值;
(Ⅲ)若存在 ,使得
,使得 ,试求
,试求 的取值范围.
的取值范围.
(本小题满分16分)已知数列 是以
是以 为公差的等差数列,数列
为公差的等差数列,数列 是以
是以 为公比的等比数列.(Ⅰ)若数列
为公比的等比数列.(Ⅰ)若数列 的前
的前 项和为
项和为 ,且
,且 ,
, ,求整数
,求整数 的值;
的值;
(Ⅱ)在(Ⅰ)的条件下,试问数列 中是否存在一项
中是否存在一项 ,使得
,使得 恰好可以表示为该数列中连续
恰好可以表示为该数列中连续 项的和?请说明理由;(Ⅲ)若
项的和?请说明理由;(Ⅲ)若 (其中
(其中 ,且(
,且( )是(
)是( )的约数),求证:数列
)的约数),求证:数列 中每一项都是数列
中每一项都是数列 中的项.
中的项.
(本小题满分14分)经市场调查,某旅游城市在过去的一个月内(以30天计),日旅游人数 (万人)与时间
(万人)与时间 (天)的函数关系近似满足
(天)的函数关系近似满足 ,人均消费
,人均消费 (元)与时间
(元)与时间 (天)的函数关系近似满足
(天)的函数关系近似满足 .(Ⅰ)求该城市的旅游日收益
.(Ⅰ)求该城市的旅游日收益 (万元)与时间
(万元)与时间 的函数关系式;(Ⅱ)求该城市旅游日收益的最小值(万元).
的函数关系式;(Ⅱ)求该城市旅游日收益的最小值(万元).
(本小题满分14分)已知角 是
是 的内角,向量
的内角,向量 ,
, ⊥
⊥ .(Ⅰ)求角A的大小;(Ⅱ)求函数
.(Ⅰ)求角A的大小;(Ⅱ)求函数 的值域.
的值域.
若直线 和直线
和直线 关于点
关于点 对称,求
对称,求 的值.
的值.