已知 ,
,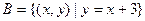 ,
, ,
,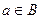 ,求
,求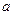 。
。
如图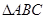 的三个顶点都在⊙O上,
的三个顶点都在⊙O上, 的平分线与BC边和⊙O分别交于点D、E.
的平分线与BC边和⊙O分别交于点D、E.
(1)指出图中相似的三角形,并说明理由;
(2)若 ,求
,求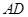 的长.
的长.
已知 ,且(1-2x)n=a0+a1x+a2x2+a3x3+……+anxn.
,且(1-2x)n=a0+a1x+a2x2+a3x3+……+anxn.
(Ⅰ)求n的值;
(Ⅱ)求a1+a2+a3+……+an的值。
规定 ,其中
,其中 ,
, 为正整数,且
为正整数,且 ,这是排列数
,这是排列数 (
( 是正整数,且
是正整数,且 )的一种推广.
)的一种推广.
(1)求 的值;
的值;
(2)排列数的两个性质:① ,②
,② (其中
(其中 是正整数).是否都能推广到
是正整数).是否都能推广到 (
( ,m是正整数)的情形?若能推广,写出推广的形式并给予证明;若不能,则说明理由;
,m是正整数)的情形?若能推广,写出推广的形式并给予证明;若不能,则说明理由;
(3)确定函数 的单调区间.
的单调区间.
工商部门对甲、乙两家食品加工企业的产品进行深入检查后,决定对甲企业的5种产品和乙企业的3种产品做进一步的检验.检验员从以上8种产品中每次抽取一种逐一不重复地进行化验检验.
(1)求前3次检验的产品中至少1种是乙企业的产品的概率;
(2)记检验到第一种甲企业的产品时所检验的产品种数共为X,求X的分布列和数学期望.
口袋中有大小、质地均相同的7个球,3个红球,4个黑球,现在从中任取3个球。
(1)求取出的球颜色相同的概率;
(2)若取出的红球数设为 ,求随机变量
,求随机变量 的分布列和数学期望。
的分布列和数学期望。