(本小题满分10分)设全集 ,
, 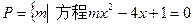 有实数根
有实数根
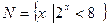 求
求 。
。
如图,已知四棱锥P-ABCD的底面为直角梯形,AD∥BC,∠BCD=900,PA=PB,PC=PD.
(I) 试判断直线CD与平面PAD是否垂直,并简述理由;
(II)求证:平面PAB⊥平面ABCD;
(III)如果CD=AD+BC,二面角P-CB-A等于600,求二面角P-CD-A的大小.
甲有一只放有x个红球,y个黄球,z个白球的箱子,乙有一只放有3个红球,2个黄球,1个白球的箱子,
(1)两个各自从自己的箱子中任取一球,规定:当两球同色时甲胜,异色时乙胜。若 用x、y、z表示甲胜的概率;
用x、y、z表示甲胜的概率;
2)在(1)下又规定当甲取红、黄、白球而胜的得分分别为1、2、3分,否则得0分,求甲得分的期望的最大值及此时x、y、z的值。
已知函数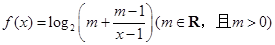 .
.
(1)求函数 的定义域;
的定义域;
(2)若函数 在
在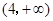 上单调递增,求
上单调递增,求 的取值范围.
的取值范围.
已知曲线 上任意一点
上任意一点 到直线
到直线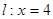 的距离是它到点
的距离是它到点 距离的
距离的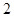 倍;曲线
倍;曲线 是以原点为顶点,
是以原点为顶点, 为焦点的抛物线.
为焦点的抛物线.
(Ⅰ)求 ,
, 的方程;
的方程;
(Ⅱ)过 作两条互相垂直的直线
作两条互相垂直的直线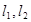 ,其中
,其中 与
与 相交于点
相交于点 ,
,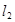 与
与 相交于点
相交于点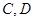 ,求四边形
,求四边形 面积的取值范围.
面积的取值范围.
已知 ,函数
,函数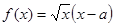 .
.
(Ⅰ)求函数 的单调区间;
的单调区间;
(Ⅱ)求函数 在区间
在区间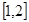 上的最小值.
上的最小值.