(本小题满分12分)已知定义在区间(-1,1)上的函数 为奇函数。且
为奇函数。且 .(1)求实数
.(1)求实数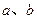 的值。
的值。
(2)求证:函数 (-1,1)上是增函数。
(-1,1)上是增函数。
(3)解关于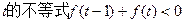 。
。
如图, 四点在同一圆上,
四点在同一圆上,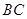 与
与 的延长线交于点
的延长线交于点 ,点
,点 在
在 的延长线上.
的延长线上.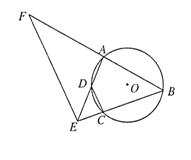
(1)若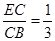 ,
,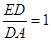 ,求
,求 的值;
的值;
(2)若 ,证明:
,证明: .
.
(本小题满分12分)已知函数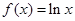 ,
,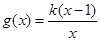 .
.
(1)当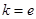 时,求函数
时,求函数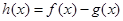 的单调区间和极值;
的单调区间和极值;
(2)若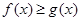 恒成立,求实数
恒成立,求实数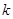 的值.
的值.
(本小题满分12分)已知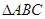 的两顶点坐标
的两顶点坐标 ,
,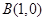 ,圆
,圆 是
是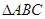 的内切圆,在边
的内切圆,在边 ,
, ,
,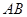 上的切点分别为
上的切点分别为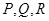 ,
, (从圆外一点到圆的两条切线段长相等),动点
(从圆外一点到圆的两条切线段长相等),动点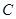 的轨迹为曲线
的轨迹为曲线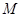 .
.
(1)求曲线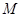 的方程;
的方程;
(2)设直线 与曲线
与曲线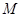 的另一交点为
的另一交点为 ,当点
,当点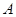 在以线段
在以线段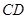 为直径的圆上时,求直线
为直径的圆上时,求直线 的方程.
的方程.
(本小题满分12分)在三棱柱 中,侧面
中,侧面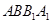 为矩形,
为矩形,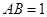 ,
,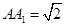 ,
,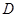 为
为 的中点,
的中点, 与
与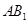 交于点
交于点 ,
, 侧面
侧面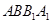 .
.
(1)证明: ;
;
(2)若 ,求三棱锥
,求三棱锥 的体积.
的体积.
(本小题满分12分)郑州市为了缓解交通压力,大力发展公共交通,提倡多坐公交少开车.为了调查市民乘公交车的候车情况,交通主管部门从在某站台等车的45名候车乘客中随机抽取15人,按照他们的候车时间(单位:分钟)作为样本分成6组,如下表所示:
(1)估计这45名乘客中候车时间少于12分钟的人数;
(2)若从上表第四、五组的5人中随机抽取2人做进一步的问卷调查,求抽到的2人恰好来自不同组的概率.