甲、乙两台机床生产同种产品,产品按质量分为一级品和二级品,为了比较两台机床产品的质量,分别用两台机床各生产了200件产品,产品的质量情况统计如下表:
一级品 |
二级品 |
合计 |
|
甲机床 |
150 |
50 |
200 |
乙机床 |
120 |
80 |
200 |
合计 |
270 |
130 |
400 |
(1)甲机床、乙机床生产的产品中一级品的频率分别是多少?
(2)能否有99%的把握认为甲机床的产品质量与乙机床的产品质量有差异?
附:
|
0.050 |
0.010 |
0.001 |
k |
3.841 |
6.635 |
10.828 |
设命题 ,若
,若 同时为假命题,求x的取值集合.
同时为假命题,求x的取值集合.
在平面直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐V标方程为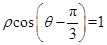 ,M,N分别为曲线C与x轴、y轴的交点.
,M,N分别为曲线C与x轴、y轴的交点.
(1)写出曲线C的直角坐标方程,并求M,N的极坐标;
(2)求直线OM的极坐标方程.
设函数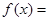 2|x-3|+|x-4|.
2|x-3|+|x-4|.
(1)求不等式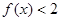 的解集;
的解集;
(2)若不等式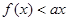 的解集不是空集,求实数a的取值范围.
的解集不是空集,求实数a的取值范围.
已知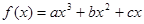 的导函数
的导函数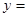
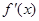 的简图,它与
的简图,它与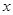 轴的交点是(0,0)和(1,0),
轴的交点是(0,0)和(1,0),
又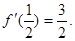
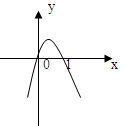
(1)求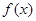 的解析式及
的解析式及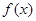 的极大值.
的极大值.
(2)若在区间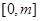 (m>0)上恒有
(m>0)上恒有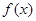 ≤x成立,求m的取值范围.
≤x成立,求m的取值范围.
已知双曲线C: 离心率是
离心率是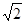 ,过点
,过点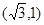 ,且右支上的弦
,且右支上的弦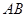 过右焦点
过右焦点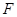 .
.
(1)求双曲线C的方程;
(2)求弦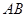 的中点
的中点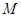 的轨迹E的方程;
的轨迹E的方程;
(3)是否存在以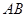 为直径的圆过原点O?,若存在,求出直线
为直径的圆过原点O?,若存在,求出直线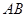 的斜率k 的值.若不存在,则说明理由.
的斜率k 的值.若不存在,则说明理由.