(本小题满分10分)
如图,已知⊙O和⊙M相交于A、B两点,AD为⊙M的直径,直线BD交⊙O于点C,点G为 中点,连结AG分别交⊙O、BD于点E、F连结CE.
中点,连结AG分别交⊙O、BD于点E、F连结CE.
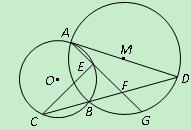
(1)求证: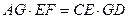 ;
;
(2)求证:
(本小题共13分)已知数列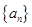 的前
的前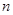 项和为
项和为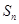 ,且
,且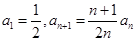 .
.
(1)求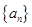 的通项公式;
的通项公式;
(2)设 ,若
,若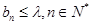 恒成立,求实数
恒成立,求实数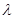 的取值范围;
的取值范围;
(3)设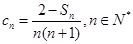 ,
,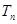 是数列
是数列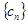 的前
的前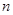 项和,证明
项和,证明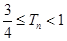 .
.
(本小题满分13分)在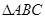 中,内角A,B,C的对边分别为
中,内角A,B,C的对边分别为 ,已知
,已知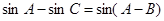 ,
,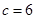 .
.
(1)求B的大小;
(2)若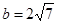 ,求
,求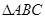 的面积;
的面积;
(3)若 的取值范围.
的取值范围.
(本小题满分10分)设等差数列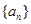 的前
的前 项和为
项和为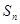 ,公差为
,公差为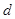 .已知
.已知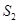 ,
,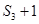 ,
,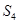 成等差数列.
成等差数列.
(1)求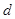 的值;
的值;
(2)若 ,
, ,
, 成等比数列,求
成等比数列,求 (
(
 )的最大值.
)的最大值.
(本小题满分10分)已知平行四边形的三个顶点的坐标为,,.
(1)求平行四边形的顶点D的坐标;
(2)在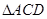 中,求CD边上的高线所在直线方程;
中,求CD边上的高线所在直线方程;
(3)求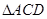 的面积.
的面积.
(本题10分) 已知:函数
(Ⅰ)求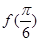 的值;
的值;
(Ⅱ)设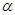 ∈(0,
∈(0,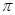 ),f(
),f(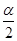 )=
)=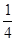 -
- ,求sin
,求sin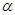 的值.
的值.