本小题满分8分)
已知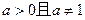 ,函数
,函数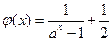 ,判断
,判断 的奇偶性,并给出证明;
的奇偶性,并给出证明;
已知:函数 的最小正周期为
的最小正周期为 (
( ),且当
),且当 时,函数
时,函数 的最小值为0,(1)求函数
的最小值为0,(1)求函数 的表达式;
的表达式;
(2)在△ABC中,若
已知函数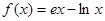 ,
,
(1)求函数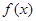 的单调区间;
的单调区间;
(2)在区间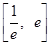 内存在
内存在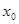 ,使不等式
,使不等式 成立,求
成立,求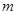 的取值范围。
的取值范围。
已知函数f(x)=Asin(ωx+φ)(x∈R,ω>0,0<φ<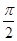 )的部分图象如图所示.
)的部分图象如图所示.
(1)求函数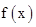 的解析式;
的解析式;
(2)求函数 的单调递增区间.
的单调递增区间.
已知函数 .
.
(1)求不等式 的解集;
的解集;
(2)设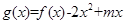 ,其中
,其中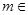 R,求
R,求 在区间
在区间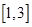 上的最小值.
上的最小值.
某气象仪器研究所按以下方案测试一种“弹射型”气象观测仪器的垂直弹射高度:在C处进行该仪器的垂直弹射,观察点A、B两地相距100m,∠BAC=60°,在A地听到弹射声音的时间比B地晚 s.A地测得该仪器在C处时的俯角为15°,A地测得最高点H的仰角为30°,求该仪器的垂直弹射高度CH.(声音的传播速度为340m/s)
s.A地测得该仪器在C处时的俯角为15°,A地测得最高点H的仰角为30°,求该仪器的垂直弹射高度CH.(声音的传播速度为340m/s)