(本小题满分14分)本题(1)、(2)、(3)三个选答题,每小题7分,任选2题作答,满分14分,如果多做,则按所做的前两题计分。作答时,先用2B铅笔在答题卡上把所选题目对应的题号涂黑,并将所选题号填入括号中。
(1)(本小题满分7分) 选修4-2:矩阵与变换
已知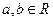 ,若
,若 所对应的变换
所对应的变换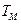 把直线
把直线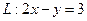 变换为自身,求实数
变换为自身,求实数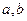 ,并求
,并求 的逆矩阵。
的逆矩阵。
(2)选修4-4:坐标系与参数方程
已知直线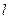 的参数方程:
的参数方程: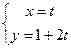 (
(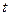 为参数)和圆
为参数)和圆 的极坐标方程:
的极坐标方程: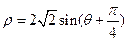 。
。
①将直线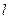 的参数方程化为普通方程,圆
的参数方程化为普通方程,圆 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
②判断直线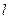 和圆
和圆 的位置关系。
的位置关系。
(3)选修4-5:不等式选讲
已知函数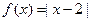
①解不等式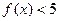 ;
;
②证明:对任意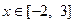 ,不等式
,不等式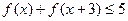 成立.
成立.
已知两点 ,点
,点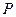 为坐标平面内的动点,且满足
为坐标平面内的动点,且满足 .
.
(Ⅰ)求点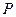 的轨迹
的轨迹 的方程;
的方程;
(Ⅱ)设过点 的直线
的直线 斜率为
斜率为 ,且与曲线
,且与曲线 相交于点
相交于点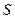 、
、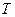 ,若
,若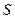 、
、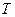 两点只在第二象限内运动,线段
两点只在第二象限内运动,线段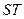 的垂直平分线交
的垂直平分线交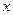 轴于
轴于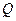 点,求
点,求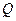 点横坐标的取值范围.
点横坐标的取值范围.
已知函数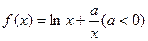 ,直线
,直线 与函数
与函数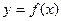 图象相切.
图象相切.
(Ⅰ)求直线 的斜率
的斜率 的取值范围;
的取值范围;
(Ⅱ)设函数 ,已知函数
,已知函数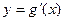 的图象经过点
的图象经过点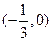 ,求函数
,求函数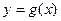 的极值.
的极值.
在数列 中,
中,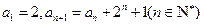 .
.
(Ⅰ)求证:数列 为等差数列;
为等差数列;
(Ⅱ)设数列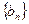 满足
满足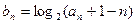 ,若
,若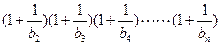
 对一切
对一切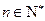 且
且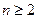 恒成立,求实数
恒成立,求实数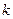 的取值范围.
的取值范围.
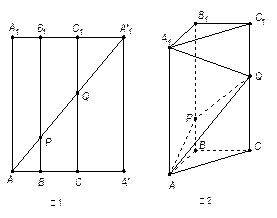 如图1所示,在边长为
如图1所示,在边长为 的正方形
的正方形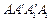 中,
中,
 ,且
,且 ,
,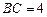 ,
, 分别交
分别交
 于点
于点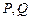 ,将该正方形沿
,将该正方形沿 、
、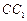 折叠,使得
折叠,使得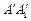 与
与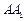 重合,构成如图2所示的三棱柱
重合,构成如图2所示的三棱柱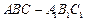 中
中
(Ⅰ)求证:
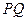 ;
;
(Ⅱ)在底边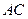 上有一点
上有一点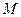 ,
,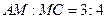 ,
,
求证: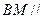 面
面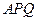
(III)求直线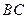 与平面
与平面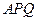 所成角的正弦值.
所成角的正弦值.
已知向量 (
(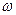 为常数且
为常数且 ),函数
),函数 在
在 上的最大值为
上的最大值为 .
.
(Ⅰ)求实数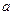 的值;
的值;
(Ⅱ)把函数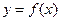 的图象向右平移
的图象向右平移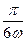 个单位,可得函数
个单位,可得函数 的图象,若
的图象,若 在
在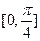 上为增函数,求
上为增函数,求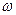 的最大值.
的最大值.