(本小题满分10分)某校数学课外兴趣小组为研究数学成绩是否与性别有关,先统计本校高三年级每个学生一学期数学成绩平均分(采用百分制),剔除平均分在30分以下的学生后,共有男生300名,女生200名.现采用分层抽样的方法,从中抽取了100名学生,按性别分为两组,并将两组学生成绩分为6组,得到如下所示频数分布表.
| 分数段 |
[40,50) |
[50,60) |
[60,70) |
[70,80) |
[80,90) |
[90,100] |
| 男 |
3 |
9 |
18 |
15 |
6 |
9 |
| 女 |
6 |
4 |
5 |
10 |
13 |
2 |
估计男、女生各自的成绩平均分(同一组数据用该组区间中点值作代表),从计算结果看,判断数学成绩与性别是否有关;
| |
优分 |
非优分 |
合计 |
| 男生 |
|
|
|
| 女生 |
|
|
|
| 合计 |
|
|
100 |
(2)规定80分以上为优分(含80分),请你根据已知条件作出 列联表,并判断是否有
列联表,并判断是否有 以上的把握认为“数学成绩与性别有关”.
以上的把握认为“数学成绩与性别有关”.
附表及公式
 |
0.100 |
0.050 |
0.010 |
0.001 |
 |
2.706 |
3.841 |
6.635 |
10.828 |
 .
.
已知点(1,2)是函数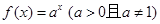 的图象上一点,数列
的图象上一点,数列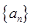 的前
的前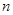 项和
项和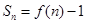 .
.
(Ⅰ)求数列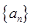 的通项公式;
的通项公式;
(Ⅱ)若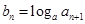 ,求数列
,求数列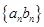 的前
的前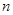 项和
项和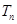 .
.
(本小题满分12分)
在△ABC中,a、b、c分别为角A、B、C所对的边,C=2A,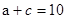 ,
, .
.
(Ⅰ)求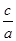 的值;
的值;
(Ⅱ)求b的值.
(本小题满分12分)
如图,海中小岛A周围40海里内有暗礁,一船正在向南航行,在B处测得小岛A在船的南偏东30°,航行30海里后,在C处测得小岛在船的南偏东45°,如果此船不改变航向,继续向南航行,问有无触礁的危险?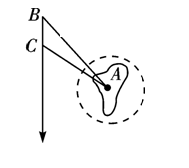
(本小题满分12分)
已知等差数列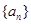 中,公差
中,公差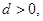 又
又 .
.
(I)求数列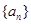 的通项公式;
的通项公式;
(II)记数列 ,数列
,数列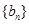 的前
的前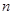 项和记为
项和记为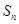 ,求
,求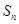 .
.
(本小题满分12分)
在锐角△ABC中,a、b、c分别为角A、B、C所对的边,且 .
.
(Ⅰ)确定角C的大小;
(Ⅱ)若c= ,且△ABC的面积为
,且△ABC的面积为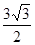
 ,求a+b的值.
,求a+b的值.