(本小题满分13分)已知椭圆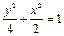 两焦点分别为
两焦点分别为 、
、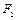 ,
,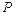 是椭圆在第一象限弧上的一点,并满足
是椭圆在第一象限弧上的一点,并满足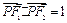 ,过点
,过点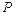 作倾斜角互补的两条直线
作倾斜角互补的两条直线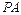 、
、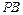 分别交椭圆于A、B两点.
分别交椭圆于A、B两点.
(1)求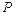 点坐标;
点坐标;
(2)证明:直线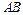 的斜率为定值,并求出该定值.
的斜率为定值,并求出该定值.
如图所示,O是线段AB的中点,|AB|=2c,以点A为圆心,2a为半径作一圆,其中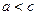 。
。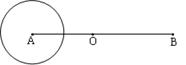
(1)若圆A外的动点P到B的距离等于它到圆周的最短距离,建立适当坐标系,求动点P的轨迹方程,并说明轨迹是何种曲线;
(2)经过点O的直线l与直线AB成60°角,当c=2,a=1时,动点P的轨迹记为E,设过点B的直线m交曲线E于M、N两点,且点M在直线AB的上方,求点M到直线l的距离d的取值范围。
已知点C为圆 的圆心,点A(1,0),P是圆上的动点,点Q在圆的半径CP上,且
的圆心,点A(1,0),P是圆上的动点,点Q在圆的半径CP上,且
(Ⅰ)当点P在圆上运动时,求点Q的轨迹方程;
(Ⅱ)若直线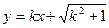 与(Ⅰ)中所求点Q的轨迹交于不同两点F,H,O是坐标原点,且
与(Ⅰ)中所求点Q的轨迹交于不同两点F,H,O是坐标原点,且 ,求△FOH的面积的取值范围。
,求△FOH的面积的取值范围。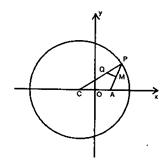
以O为原点, 所在直线为
所在直线为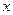 轴,建立如 所示的坐标系。设
轴,建立如 所示的坐标系。设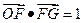 ,点F的坐标为
,点F的坐标为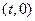 ,
, ,点G的坐标为
,点G的坐标为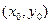 。
。
(1)求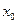 关于
关于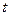 的函数
的函数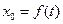 的表达式,判断函数
的表达式,判断函数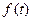 的单调性,并证明你的判断;
的单调性,并证明你的判断;
(2)设ΔOFG的面积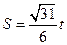 ,若以O为中心,F为焦点的椭圆经过点G,求当
,若以O为中心,F为焦点的椭圆经过点G,求当 取最小值时椭圆的方程;
取最小值时椭圆的方程;
(3)在(2)的条件下,若点P的坐标为 ,C、D是椭圆上的两点,且
,C、D是椭圆上的两点,且 ,求实数
,求实数 的取值范围。
的取值范围。
已知双曲线 的左右两个焦点分别为
的左右两个焦点分别为 ,点P在双曲线右支上.
,点P在双曲线右支上.
(Ⅰ)若当点P的坐标为 时,
时,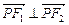 ,求双曲线的方程;
,求双曲线的方程;
(Ⅱ)若 ,求双曲线离心率
,求双曲线离心率 的最值,并写出此时双曲线的渐进线方程.
的最值,并写出此时双曲线的渐进线方程.
在平面直角坐标系内有两个定点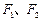 和动点P,
和动点P,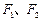 坐标分别为
坐标分别为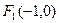 、
、 ,动点
,动点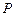 满足
满足 ,动点
,动点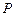 的轨迹为曲线
的轨迹为曲线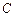 ,曲线
,曲线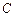 关于直线
关于直线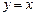 的对称曲线为曲线
的对称曲线为曲线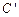 ,直线
,直线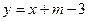 与曲线
与曲线 交于A、B两点,O是坐标原点,△ABO的面积为
交于A、B两点,O是坐标原点,△ABO的面积为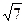 ,
,
(1)求曲线C的方程;(2)求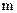 的值。
的值。