已知函数 ,
, .
.
(1)求 的值;
的值;
(2)求函数 的极大值.
的极大值.
已知抛物线的顶点在原点,对称轴为 轴,焦点在双曲线
轴,焦点在双曲线 上,求抛物线方程.
上,求抛物线方程.
椭圆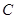 的中心在原点,焦点在坐标轴上,经过
的中心在原点,焦点在坐标轴上,经过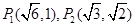
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)斜率不为 的直线
的直线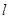 与椭圆
与椭圆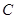 交于
交于 、
、 两点,定点
两点,定点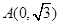 ,若
,若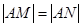 ,求直线
,求直线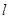 的斜率
的斜率 的取值范围.
的取值范围.
设椭圆C:
 的离心率与双曲线x2-y2=1的离心率互为倒数,且
的离心率与双曲线x2-y2=1的离心率互为倒数,且 在椭圆上.
在椭圆上.
(Ⅰ) 求椭圆C的方程;
(Ⅱ) 若椭圆C左、右焦点分别为 ,过
,过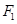 的直线
的直线 与椭圆C相交于
与椭圆C相交于 两点,求
两点,求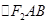 面积的最大值.
面积的最大值.
如图,四棱锥P—ABCD中,底面ABCD为矩形,PA⊥底面ABCD,PA=AB,点E是PB的中点,点F是EB的中点.
(Ⅰ) 求证: 平面
平面 ;
;
(Ⅱ) 求证: 平面
平面 .
.