已知函数 的图象在
的图象在 上连续,定义:
上连续,定义: ,
, .其中,
.其中, 表示函数
表示函数 在
在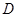 上的最小值,
上的最小值,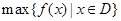 表示函数
表示函数 在
在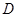 上的最大值.若存在最小正整数
上的最大值.若存在最小正整数 ,使得
,使得 对任意的
对任意的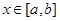 成立,则称函数
成立,则称函数 为
为 上的“
上的“ 阶收缩函数”.
阶收缩函数”.
(Ⅰ)若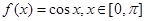 ,试写出
,试写出 ,
, 的表达式;
的表达式;
(Ⅱ)已知函数 ,试判断
,试判断 是否为
是否为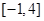 上的“
上的“ 阶收缩函数”.如果是,求出对应的
阶收缩函数”.如果是,求出对应的 ;如果不是,请说明理由;
;如果不是,请说明理由;
(Ⅲ)已知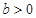 ,函数
,函数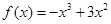 是
是 上的2阶收缩函数,求
上的2阶收缩函数,求 的取值范围.
的取值范围.
(本小题满分12分)已知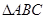 中,
中,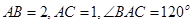 ,
,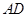 为角分线.
为角分线.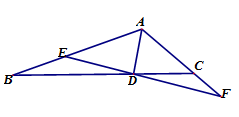
(Ⅰ)求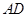 的长度;
的长度;
(Ⅱ)过点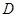 作直线交
作直线交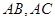 于不同两点
于不同两点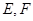 ,且满足
,且满足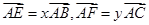 ,求证:
,求证: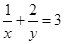 .
.
(本小题满分12分)已知数列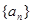 的前
的前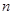 项和
项和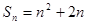 (
(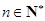 ),数列
),数列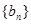 的前
的前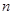 项和
项和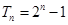 (
(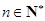 ).
).
(Ⅰ)求数列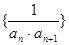 的前
的前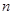 项和;
项和;
(Ⅱ)求数列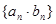 的前
的前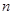 项和.
项和.
(本小题满分12分)已知向量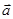 ,
,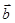 满足
满足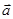
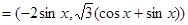 ,
,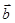
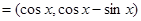 ,函数
,函数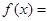
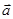 ·
·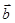
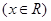 .
.
(Ⅰ)将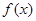 化成
化成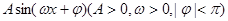 的形式;
的形式;
(Ⅱ)求函数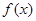 的单调递减区间;
的单调递减区间;
(Ⅲ)求函数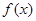 在
在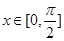 的值域.
的值域.
(本小题满分10分)在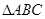 中,角
中,角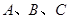 对边分别为
对边分别为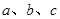 ,且
,且 .
.
(Ⅰ)求角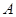 ;
;
(Ⅱ)若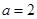 ,求
,求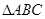 周长的取值范围.
周长的取值范围.
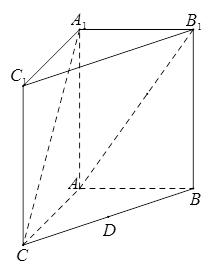
如图,在三棱柱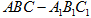 中,四边形
中,四边形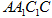 是边长为4的正方形,平面
是边长为4的正方形,平面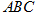 ⊥平面
⊥平面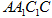 ,
,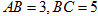 .
.
(Ⅰ)求证: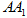 ⊥平面
⊥平面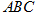 ;
;
(Ⅱ)若点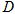 是线段
是线段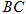 的中点,请问在线段
的中点,请问在线段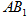 是否存在点
是否存在点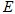 ,使得
,使得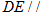 面
面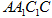 ?若存在,请说明点
?若存在,请说明点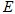 的位置,若不存在,请说明理由;
的位置,若不存在,请说明理由;
(Ⅲ)求二面角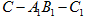 的大小.
的大小.