在平面直角坐标系xOy中,已知对于任意实数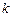 ,直线
,直线 恒过定点F. 设椭圆C的中心在原点,一个焦点为F,且椭圆C上的点到F的最大距离为
恒过定点F. 设椭圆C的中心在原点,一个焦点为F,且椭圆C上的点到F的最大距离为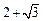 .
.
(1)求椭圆C的方程;
(2)设(m,n)是椭圆C上的任意一点,圆O: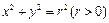 与椭圆C有4个相异公共点,试分别判断圆O与直线l1:mx+ny=1和l2:mx+ny=4的位置关系.
与椭圆C有4个相异公共点,试分别判断圆O与直线l1:mx+ny=1和l2:mx+ny=4的位置关系.
已知 的展开式中第2项的二项式系数与第3项的二项式系数之比为1:7.
的展开式中第2项的二项式系数与第3项的二项式系数之比为1:7.
(1)、求n的值;
(2)、有理项共有哪几项。
已知向量a=(
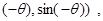 b
b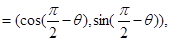
(1)求证:a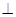 b
b
(2)若存在不等于0的实数k和t,使x=a+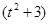 b, y=
b, y= ka+tb满足x
ka+tb满足x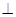 y,试求此时
y,试求此时 的最小值.
的最小值.
已知函数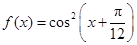 ,
,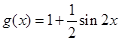 .
.
(1)设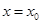 是函数
是函数 图象的一条对称轴,求
图象的一条对称轴,求 的值;
的值;
(2)求函数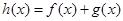 的单调递增区间.
的单调递增区间.
已知A、B、C三点的坐标分别是A(3,0),B(0,3),C ,其中
,其中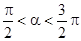 ,
,
(1)若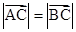 ,求角
,求角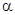 的值;
的值;
(2)若 ,求
,求 的值.
的值.
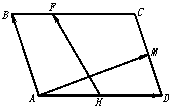
如图,平行四边形ABCD中,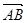 =a,
=a,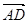 =b,H、M是AD、DC之中点,F使BF=
=b,H、M是AD、DC之中点,F使BF= BC,(1)以a、b为基底表示向量
BC,(1)以a、b为基底表示向量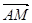 与
与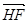 ;(2)若|a|=3,|b|=4,a与b的夹角为
;(2)若|a|=3,|b|=4,a与b的夹角为 ,求
,求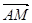

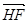 .
.