已知椭圆C: 的左右焦点分别为
的左右焦点分别为 ,点B为椭圆与
,点B为椭圆与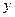
轴的正半轴的交点,点P在第一象限内且在椭圆上,且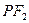 与
与 轴垂直,
轴垂直,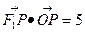
(1)求椭圆C的方程;
(2)设点B关于直线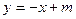 的对称点E(异于点B)在椭圆C上,求
的对称点E(异于点B)在椭圆C上,求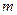 的值。
的值。
设函数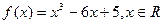 .
.
(1)求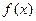 的单调区间和极值;
的单调区间和极值;
(2)若关于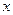 的方程
的方程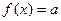 有3个不同实根,求实数a的取值范围.
有3个不同实根,求实数a的取值范围.
(3)已知当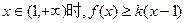 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.
已知数列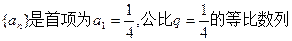 ,设
,设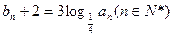 ,数列
,数列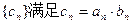 。
。
(1)求证: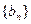 是等差数列;
是等差数列;
(2)求数列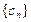 的前n项和
的前n项和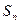 ;
;
某单位为绿化环境,移栽了甲、乙两种大树各2株.设甲、乙两种大树移栽的成活率分别为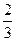 和
和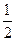 ,且各株大树是否成活互不影响.求移栽的4株大树中:
,且各株大树是否成活互不影响.求移栽的4株大树中:
(1)两种大树各成活1株的概率;
(2)成活的株数 的分布列与期望.
的分布列与期望.
设函数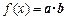 ,其中向量
,其中向量 ,
, ,
, ,且
,且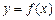 的图象经过点
的图象经过点 .(Ⅰ)求实数
.(Ⅰ)求实数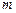 的值;(Ⅱ)求函数
的值;(Ⅱ)求函数 的最小值及此时
的最小值及此时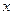 值的集合.
值的集合.
对于正整数 ,用
,用 表示
表示 的最大奇因数,如:
的最大奇因数,如: ,……. 记
,……. 记 ,其中
,其中 是正整数.
是正整数.
(I)写出 ,
,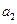 ,
, ,并归纳猜想
,并归纳猜想 与
与
 N)的关系式;
N)的关系式;
(II)证明(I)的结论;
(Ⅲ)求 的表达式.
的表达式.